Análise Matemática I - Engª
Mecânica
![]()
![]()
12 de Fevereiro de 2004
Duração:
2h 30m
Sem consulta de
apontamentos ou textos. Tabela autorizada.
Calculadora
gráfica obrigatória.
Importante: Deve justificar
adequadamente os passos seguidos na resolução de cada questão,
mesmo quando use a calculadora gráfica.
1- Resolva a seguinte
equação diferencial linear de primeira ordem, usando o
método da variação das constantes arbitrárias:
![]()
2- Escreva os integrais que nos
permitem calcular o volume (mas não o calcule) do sólido de
revolução obtido a partir da rotação da figura
delimitada pelas curvas definidas pelas seguintes equações:
![]()
em torno do eixo dos XX.
3- Calcule:
a)
![]()
b) ![]()
c)
![]()
4- Considere a
função f definida por:
f(x) = 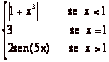
a) Calcule f ’(x);
b) Determine
os extremos relativos de f, caso existam;
c) Esboce um
gráfico de f ; no gráfico de f assinale sem ambiguidade todos
os extremos determinados na alínea anterior;
d)
Calcule ![]() .
.
5- a) Considere o
seguinte campo de direcções da equação diferencial ![]() . Determine graficamente a solução
. Determine graficamente a solução ![]() que
passa pelo ponto (1,1).
que
passa pelo ponto (1,1).
Nota: responda a esta
alínea na folha de resposta anexa.
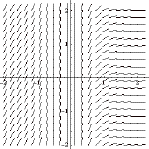
b) Explique o que
acontece junto da recta x=0 .
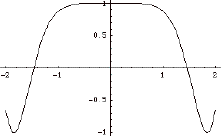
6- Considere a
função ![]() definida pela
representação gráfica junta:
definida pela
representação gráfica junta:
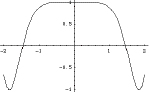
a) Esboce o gráfico
da derivada de ![]() no intervalo [-2
, 1]
no intervalo [-2
, 1]
b) Esboce, no intervalo [-2
, 2], o gráfico da
função ![]() definida por
definida por ![]() .
.
Nota: responda na
folha de resposta anexa.

7• Um fio
eléctrico ligando um poste a uma casa tem a forma de uma
catenária de equação ![]() . Sabendo que o poste tem 3 metros de altura, que a
catenária intersecta o eixo dos YY no ponto (0,2), onde as unidades
estão em metros, que a base do poste está a 2 metros do eixo dos
YY e que o ponto da casa onde liga o fio está a 1 metro de
distância do eixo dos YY, determine o comprimento do fio desde a casa
até ao poste.
. Sabendo que o poste tem 3 metros de altura, que a
catenária intersecta o eixo dos YY no ponto (0,2), onde as unidades
estão em metros, que a base do poste está a 2 metros do eixo dos
YY e que o ponto da casa onde liga o fio está a 1 metro de
distância do eixo dos YY, determine o comprimento do fio desde a casa
até ao poste.
Folha de resposta (não esquecer de anexar ao caderno de
respostas)
Nome:____________________________________________________________ Nº
de aluno:_________
Modelo de calculadora gráfica usado:
___________________________________________
Análise Matemática I - Engª
Mecânica
![]()
![]()
12 de Fevereiro de 2004
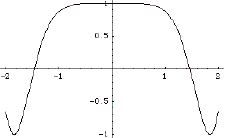
5- a) 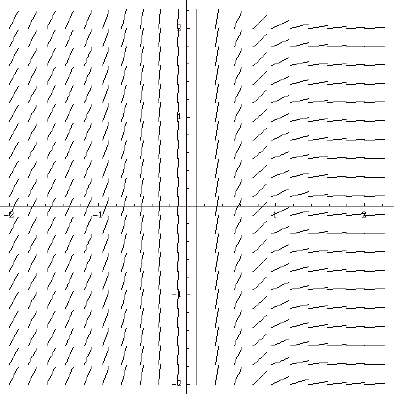
6- a) b)