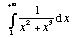
2(a) frequência Análise Matemática I Eng(a) Mecânica
Análise Matemática I - Eng(a) Mecânica
19 de Junho de 1996
Duração: 3 horas
Sem consulta de apontamentos ou textos
Tabela autorizada
Calculadora científica ou gráfica autorizada
1- Indique a natureza do seguinte integral impróprio
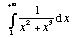
2- a) Esboce a região do plano limitada inferiormente
pela curva definida pela expressão analítica
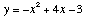 e superiormente pela tangente à curva no ponto
(0,-3) e pela recta definida por
e superiormente pela tangente à curva no ponto
(0,-3) e pela recta definida por 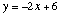 .
.
b) Calcule a área da região plana referida.
3- Considere a função real de variável real definida por:
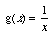
a) Desenvolva-a em série de potências de
x -2
b) Determine o intervalo de convergência da série
obtida.
c) Por que não se pode desenvolver a função
g em série de potências de x ?
d) Use a alínea a) para determinar
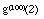
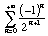
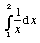
4- Determine a natureza das séries numéricas seguintes:
a) 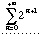
b) 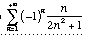
c) 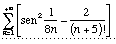
5- Seja 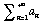 uma série numérica de termos positivos.
Seja g uma função definida por
uma série numérica de termos positivos.
Seja g uma função definida por
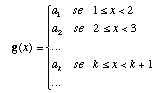
i) f(k) = ak ;
ii) o domínio de f é [1,+(inf)[ ;
iii) f é positiva ;
iv) f é decrescente .
a) Prove que o termo geral Sk da sucessão associada à série dada é igual a
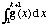 .
.
b) Prove que a série será convergente
se e só se o integral impróprio
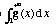 for convergente.
for convergente.
c) Prove que 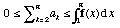 .
.
d) O que pode concluir da alínea anterior?
6- Quando estava a escrever a 2(a) frequência, tracei o gráfico de uma função f para pedir a determinação da área da figura obtida. Como o Destino fez cair um "borrão" no meu desenho tive de alterar o problema.
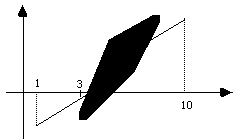
a) 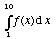
b) 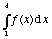
c) 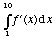
d) 
This page was created using TextToHTML. TextToHTML is a free software for Macintosh and is (c) 1995,1996 by Kris Coppieters, e-mail: 100025.2724@compuserve.com