Home Page

DECORAR A TABUADA OU UTILIZAR AS CALCULADORAS?

Nos últimos anos tem-se assistido a um espectacular progresso da indústria electrónica, que tem tido como consequência imediata a existência de calculadoras cada vez mais poderosas e, sobretudo, a preços cada vez mais acessíveis.

A grandeza de tal evolução está bem retratada nas seguintes palavras de Toffler: "Se, a indústria automóvel tivesse progredido o que a indústria da computação progrediu nos últimos 30 anos, um Rolls-Royce custaria 150 escudos e andaria 500 mil quilómetros com um litro de gasolina".

É certo que actualmente, em Portugal, os preços ainda não são muito acessíveis para a grande maioria da população; no entanto, a evolução no sentido da acessibilidade é irreversível, e penso que nos deveremos preparar para o impacto que tal facto terá (se é que não começa já a ter) no ensino da matemática.

Nesta pequena nota pretendo expôr alguns dos problemas, vantagens e consequências da utilização de calculadoras no ensino da Matemática desde o jardim de infância à Universidade.

Não tenho a pretensão de ser exaustivo, muito menos a de propôr soluções para Portugal, mas apenas a de levantar algumas questões (muito gerais, devido à grande extensão e delicadeza do assunto) confiando no velho provérbio:"Homem prevenido vale por dois". E se a experiência de outros países não deve ser decalcada, deve ser estudada para que não se caia nos mesmos erros e se possam aproveitar todas as potencialidades.

Antes de continuar, é necessário aclarar o que entendo por calculadora; tenho vindo a empregar essa designação num sentido lato, como "maquina de fazer cálculos". Há que distinguir entre as chamadas calculadoras electrónicas (programáveis ou não) e os computadores (micro, mini e grandes computad()res). As primeiras efectuam as quatro operações fundamentais e calculam um certo número de funções (trigonométricas, logaritmo, etc .) ; as programáveis permitem efectuar uma determinada sequência de um número reduzido de operações através de uma linguagem muito simples. Os computadores permitem fazer tudo isso e muito mais, melhor e mais depressa.

Para o ensino, têm interesse as calculadoras pela sua facilidade de utilização e baixo preço, e os microcomputadores devido ao interessante equilíbrio entre uma grande capacidade e um preço bastante acessível.

Claro que nos poderemos perguntar se trará algum beneficio a introdução das calculadoras e computadores na aula de matemática. Mesmo que se pense que não, teremos de concordar com C. Creenes: "Com a difusão que estes têm, é essencial que os alunos aprendam a usá-los". Claro que a sua difusão não pode ser incontrolada pois, caso contrário, acontecerá o que F.F. Bonsal1 muito justamente assinala: "Talvez os poderes matemáticos da raça humana se atrofiem, se ela levar uma vida fácil e de conforto, e depender das calculadoras na escola".

E nem se podem ignorar as limitações inerentes a tais máquinas, nem que só se tirarão benefícios se a sua utilização fizer parte de um curriculum devidamente estruturado.

Passemos pois a uma breve análise das questões relacionadas com a introdução das calculadoras na aula de matemática, e em seguida dos computadores.

Existem estudos que mostram a utilidade das calculadoras no ensino da contagem no jardim de infância e que, ao contrário do que se poderia supôr, as crianças apreendem bem o significado do "carregar no botão".

Já na escola primária as possibilidades são mais diversas: verificação imediata das respostas a problemas, exploração de padrões de números, cálculos com números grandes, estimativas da ordem de grandeza dos círculos, etc..

Na escola secundária as aplicações são quase ilimitadas: resolução de problemas com cálculos demasiados longos para serem feitos à mão, motivação das partes mais abstractas da álgebra devido à grande rapidez dos cálculos, verificação da velocidade de convergência de uma sucessão; utilização como uma espécie de "laboratório matemático": procura de padrões, formulação de conjecturas, teste de hipóteses, explicação de regularidades; as calculadoras justificam o interesse de operações como

Existem inúmeros estudos sobre as consequências da introdução das calculadoras na aula (em [7] é descrita um experiência no 10º ano de escolaridade). É de notar que se está longe de uma unanimidade nas conclusões: uns concluem que não há diferenças significativas ao nivel da aprendizagem, da retenção dos conhecimentos, ou do interesse pela matemática; outros concluem que as calculadoras trazem benefícios (por vezes só a certas categorias de alunos).

No entanto, globalmente, o saldo é considerado positivo, pois o N.C.T.Y. (Associação Americana dos Professores de Matemática) na sua Agenda de Acção para os anos 80 recomenda, em 3º lugar, que se "explorem todas as vantagens oferecidas pelos computadores e calculadoras" em todos os graus de ensino.

É altura de referir que não se trata de substituir a tabuada pela calculadora, de modo nenhum! Trata-se, sim, de auxiliar o ensino da matemática tornando-o mais "prático" (no fundo, de acordo com o provérbio chinês: "Ouço e esqueço-me. Vejo e lembro-me. Faço e compreendo.").

Já os computadores (referirme-ei quase sempre a microcomputadores pois actualmente são, de longe, os mais utilizados com fins educativos) oferecem possibilidades muito mais vastas, para não dizer espectaculares, sobretudo se considerarnos o seu preço. Em contrapartida, as dificuldades ou "perigos" da sua utilização são consideravelmente miores.

Uma das maiores vantagens dos computadores é a de poderem adaptar o ensino às necessidades, dificuldades e compreensão de cada aluno. Claro que, salvo em casos pontuais, o computador não pode assegurar por si só o ensino pois as aulas "ao vivo" são insubstituíveis. É por isso que o ensino por computador é genericamente designado por C.A.I. ( Computer Assisted Instruction * Ensino Assistido por Computador). Esse ensino pode revestir inúmeras formas, das quais citarei as três mais importantes:

    - ensino programado
    - simulação
    - resolução de problemas ("solving problems")

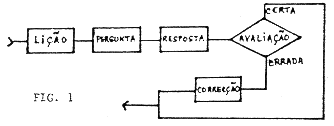
O ensino programado, adequado para o ensino de matérias para as quais se consegue construir uma sequência de componentes elementares, pode ser resumdio no esquema da Fig. 1.

A simulação é um modo de ana1isar um tema usando uma representação ou modelo de uma situação e depois fazendo-o "funcionar" de modo a observar o seu comportamento segundo várias circunstâncias (um exemplo é descrito em [3]); a simulação permite pois abordar por uma via de tipo experimental o estudo de fenómenos demasiado complexos, caros ou perigosos (por exemplo a síntese da nitroglicerina!)

Já a resolução de problemas é um trunfo claro do computador: posto o aluno perante um determinado problema que devera resolver, o computador ir-lhe-á indicando se as suas tentativas de resolução, totais ou parciais, levam a algum lado, permitindo que o aluno progrida ao seu ritmo próprio e saiba imediatamente os porquês dos seus fracassos.

Poderá parecer à primeira vista que futuramente o professor nada mais terá a fazer.

Pelo contrário! Tal como há circunstâncias em que um aluno aprende melhor sozinho, há outras em que não pode dispensar actividades em pequenos ou grandes grupos sob a orientação do professor.Uma das condições necessárias para o êxito do C.A.I. é mesmo uma correcta orientação do aluno que só o professor pode dar. Mas que o papel do professor poderá mudar radicalmente nos próximos anos, isso é verdade. Vejamos mais detalhadamente os probelmas inerentes ao C.A.I.

Se o ensino programado é acusado de precisar de supersimplificar um assunto para este poder ser decomposto em "átomos", já a simulação é de muito mais difícil execução pois pretende dar uma boa "imitação" (e simples) da realidade, com todos os seus imprevistos. A resolução, de problemas é talvez o de mais fácil implementação, mas cobre apeanas uma parte do ensino.

É de referir que em Portugal já se fazem experiências de C.A.I., pelo menos na Universidade do Minho ([6]).

O C.A.I. além de permitir adequar o ensino às necessidades de cada aluno, permite ainda controlar de maneira contínua certas fases do processo ensino-aprendizagem (o professor pode consultar no computador o registo das reacções dos alunos às questões formuladas), além de que o aluno, ficando com o registo da "conversa" que teve com o computador, pode relê-la posteriormente, para melhor se aperceber dos seus erros. É preciso não ignorar o perigo de impessoalização e stardardização, e o de se acentuar demasiado o raciocínio lógico em detrimento do intuitivo.

Mas só se poderão extrair benefícios e minorar os inconvenientes se a elaboração dos programas do C A. I. der o devido peso às componentes- científica, pedagógica e informática, não esquecendo a indispensável articulação entre o ensino do professor e o do computador. Deve-se meditar no facto de 1 hora de C.A.I. levar entre 10O a 300 horas a ser elaborada!

Não posso deixar de referir ainda três aspectos da utilização dos computadores no ensino

O primeiro diz respeito às novas perspectivas abertas ao ensino da geometria pelas espantosas capacidades gráficas dos computadores, de que um dos exemplos mais conhecidos é a célebre "Tartaruga" de Seymor Papert.

O segundo diz respeito à avaliacão da aprendizagem por meio do computador, campo em que têm sido obtidos resultados bastante positivos ([4]).

Por último, uma possibilidade espectacular mas de conseuqências totalemente imprevísiveis: por cerca de 5500$00 pode-se comprar um programa chamado muMATH que permite fazer cálculos com números racionais comm 611 dígitos significativos, calcular derivadas de funcções de uma ou mais variáveis, clacular primitivas (não todas, claro), desenvolver funções em série, simplificar os resultados, etc. Os problemas levantados por este e outros desenvolvimentos das técnicas de computação põem inúmeras questões no campo do ensino. Aqui deixo uma: Poder-se-á proibir o uso dos computadores para fazer o trabalho de casa?

BILIOGRAFIA EM INGLÊS