• Nutação

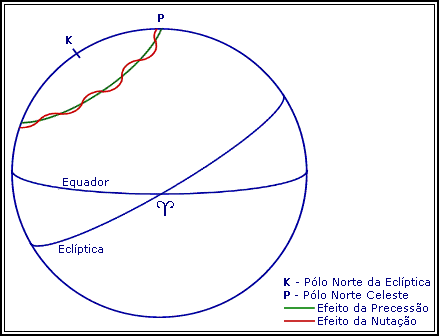
    A nutação, descoberta pelo astrónomo britânico James Bradley (1693 - 1762), é uma oscilação periódica do eixo de rotação da Terra em torno da sua posição "média". Devido à nutação, o pólo instantâneo da rotação da Terra oscila à volta de um pólo "médio" que avança devido à precessão em torno do pólo da eclíptica.

Fig. 01: Esquema do Efeito da Precessão e da Nutação.

    A nutação está associada, principalmente, à acção da Lua e pode ser descrita como a soma de uma série de vários termos. O termo mais importante tem um período de 6798.4 dias (18.6 anos), mas alguns dos outros termos têm um período muito curto (menor que 10 dias).

    A nutação encontra-se convenientemente repartida em duas componentes, uma paralela e outra perpendicular à eclíptica. A componente ao longo da eclíptica é denotada por Dy e denomina-se por Nutação em Longitude, esta afecta a longitude celeste de todos os corpos celestes.  A componente perpendicular à elíptica denota-se por De e dá pelo nome de Nutação em Obliquidade, visto que afecta a obliquidade do Equador relativamente à Eclíptica. Há no entanto que realçar que o efeito da nutação não afecta a latitude dos corpos celestes.

    As componentes Dy e De podem ser calculadas através do seguinte procedimento:

        T = (DJE - 2451545)/36525

        D = 297.85036 + 445267.111480T - 0.0019142T² + T³/189474

        M = 357.52772 + 35999.050340T - 0.0001603T² - T³/300000

        M' = 134.96298 + 477198.867398T + 0.0086972T² + T³/327270

        F = 93.27191+483202.017538T - 0.0036825T² + T³/327270

        W = 125.04452 - 1934.136261T + 0.0020708T² + T³/450000

    A nutação em longitude Dy e em obliquidade De são então obtidas através da soma dos termos dados numa tabela presente em “1980 IAU Theory of Nutation” (Ibid página S23).

    É obvio que não havendo necessidade de grande precisão, é possível o uso de apenas os termos periódicos com os maiores coeficientes. Se uma precisão 0’’.5 em Dy e 0’’.1 em De for suficiente, então pode-se desprezar os termos em T² e em T³ na expressão de W. Assim sendo obtêm-se as seguintes expressões:

Dy = -17''.20sin(W) - 1''.32sin(2L) - 0''.23sin(2L') + 0''.21sin(2W)

De = 9''.20cos(W) + 0''.57cos(2L) + 0''.10cos(2L') - 0''.09cos(2W)

    Onde L e L’ representam as longitudes médias do Sol e da Lua, respectivamente.

L=280º.4665+36000º.7698T

L’=218º.3165+481267º.8813T

    • Obliquidade da Eclíptica:

    A obliquidade da eclíptica é o ângulo entre o equador e a eclíptica. É preciso fazer a distinção entre obliquidade média e verdadeira, sendo o ângulo que a eclíptica faz com o equador médio e verdadeiro, respectivamente. Noutras palavras, o adjectivo médio indica que a correcção do efeito da nutação não é tido em conta.

    A obliquidade média da eclíptica é dada pela seguinte fórmula:

e₀ = 23º26'21''.448 - 46''.8150T - 0''.00059T² + 0''.001813T³

(fórmula adoptada pela União Astronómica Internacional)

    A precisão da fórmula anterior não é satisfatória para um longo período de tempo, já que após 2000 anos o erro é de cerca de 10’’. Torna-se então necessário a adopção de uma nova fórmula melhorada (Fórmula descoberta por J. Laskar, "Astronomy and Astrophysics", Vol. 157, página 68 (1986)).

    Seja U=T/100, tem-se então:

e₀ = 23º26'21''.448 - 4680.93U - 1.55U² + 1999.25U³ - 51.38U⁴

- 249.67U⁵ - 39.05U⁶ + 7.12U⁷ + 27.87U⁸ + 5.79U⁹ + 2.45U¹⁰

    Após 1000 anos a precisão da fórmula anterior é de cerca de 0.’’01 e apenas alguns segundos após 10000 anos. No entanto esta fórmula apenas é válida para um período de 10000 anos para cada lado da época inicial (J2000.0).

    Como curiosidade, é apresentado um gráfico da variação de e₀ desde 10000 anos antes a 10000 anos depois de J2000.0.

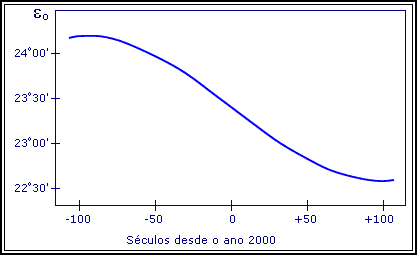
Fig. 02: Gráfico com a variação da Obliquidade Média da Eclíptica durante 200 séculos.

    A obliquidade verdadeira da eclíptica é e ₌ e₀ + De, onde De representa a nutação em obliquidade.

    • Correcções a efectuar na posição da Estrela:

    A maneira mais simples e mais directa de aplicar o efeito da nutação à posição média é adicionar Dy à longitude eclíptica dos objectos. Este procedimento poderá ser usado no cálculo das posições dos planetas, mas para as estrelas é preferível determinar as correcções em ascensão recta e declinação.

     As correcções de primeira ordem à ascensão recta a e à declinação d de uma estrela devido à nutação são:

Da₁ = (cos(e) + sin(e)sin(a)tan(d))Dy - (cos(a)tan(d))De

Dd₁ = (sin(e)cos(a))Dy + sin(a)De

    Estas expressões são inválidas para estrelas próximas de algum dos pólos celestes. Neste caso é preferível trabalhar em coordenadas eclípticas e simplesmente adicionar Dy à longitude.