As paralaxes estrelares são um factor muito importante na Astronomia.

    ...como George Lovi escreveu...

    De seguida é apresentada uma figura que tenta esquematizar a paralaxe estrelar:

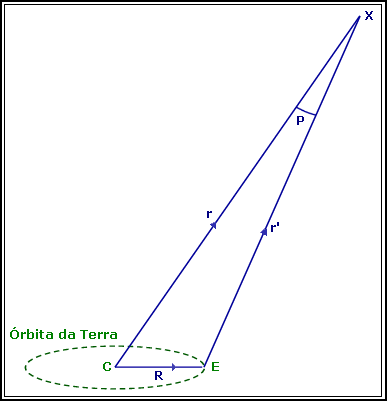
Fig. 01: Paralaxe Estrelar.

    Seja X a posição do corpo celeste, C o baricentro do sistema solar e E o centro da Terra. Sejam ainda r e R os vectores posição baricêntricos do objecto e da Terra respectivamente e r' o vector posição geocêntrico do objecto. O ângulo entre os vectores r e r' é a Paralaxe Anual p.

    Obviamente tem-se que r = r' + R. No caso de X ser um corpo dentro do sistema solar, é essencial usar a fórmula anterior conforme é apresentada, no entanto, se for uma estrela, algumas simplificações poderão ser feitas. A paralaxe irá então variar ao longo do ano assim como a Terra descreve a sua órbita em torno do Sol.

    Seja E a elongação da estrela a partir do Sol, isto é, E=CÊX, então

sinp = (R/r)sinE

    A paralaxe estrelar é geralmente definida por p, onde:

sinp = 1/r

    com r expresso em unidades astronómicas. Este valor corresponde à paralaxe anual quando R=1 e E=90º.

    No entanto, para quem necessita de calcular posições de estrelas precisas, a paralaxe estrelar não é relevante. Felizmente, as paralaxes estrelares nunca excedem os 0''.8 e podem ser negligenciadas na maioria dos casos. De acordo com R. Burnham, apenas 13 estrelas com magnitude superior a 9.0 se encontram a menos de 13 anos-luz (4 parsec) e possuem uma paralaxe que ultrapassa os 0''.25, são elas:

    Devido à paralaxe das estrelas ser sempre inferior a 0''.8, a distância da Terra à Estrela poderá ser calculada, com suficiente precisão através de:

d = 1/p

    Esta distância é em geral muito grande, pelo que convém usar unidades adequadas. A unidade mais comum é o parsec, que corresponde a uma paralaxe de um segundo de arco. Se p for expresso em radianos, então pela fórmula anterior obtém-se a distância em unidades astronómicas, mas, se p for expresso em segundos de arco, a distância é obtida em parsecs.