Lua - Introdução e Coordenadas
![]()
A Lua é o único satélite natural da Terra. As suas características médias são:
Órbita: 384400km (à volta da Terra);
Diâmetro: 3476 km;
Massa: 7.35´1022kg;
Os Romanos chamavam-lhe Luna e os Gregos Selene e Artemis.
• Coordenadas da Lua
O movimento da Lua é, principalmente, devido a dois corpos - o Sol e a Terra. No entanto, para calcular a posição correcta da Lua a cada instante torna-se necessário ter em conta centenas de termos periódicos na sua longitude, latitude e distância.
Em seguida vai-se descrever um algoritmo que, utilizando um menor número de termos, terá uma precisão de 10'' em longitude e 4'' em latitude. Para se obter uma melhor precisão deverá consultar o método presente em "Lunar Tables and Programs".
Os termos periódicos usados neste capítulo são baseados na “Teoria Lunar 2000/82” de Chapront, sendo que os usados para os argumentos médios L', D, M, M' e F foram usados as expressões melhoradas, mais tarde, por Chanpront.
Primeiramente calculam-se os seguintes valores:
L' = 218.3164477 + 481267.88123421T - 0.0015786T2 + T3/538841 - T4/65194000
D = 297.8501921 + 445267.1114034T - 0.0018819T2 + T3/545868 - T4/113065000
M =357.5291092 + 35999.0502909 - 0.0001536T2 + T3/24490000
M' = 134.9633964 + 477198.8675055T + 0.0087414T2 + T3/69699 - T4/14712000
F = 93.2720950 + 483202.0175233T - 0036539T2 - T3/3526000 + T4/863310000
A1 = 119º.75 + 131º.849T
A2 = 53º.09 + 479264º.290T
A3 = 313º.45 + 481266º.484T
Nota: Note-se que T encontra-se expresso em séculos e deverá ser calculado com muita precisão, pelo menos nove casas decimais, visto que em 0.000000001 séculos (aproximadamente três segundos) a Lua move-se cerca de 1.7 segundos de arco!
Nota 2: Estes valores deverão vir expressos em graus, e para evitar ângulos muito grandes é conveniente reduzi-los a menos de 360º.
Estes valores irão servir para calcular os valores de Sl, Sr e Sb. Estes valores correspondem à soma de vários termos que resultam de uma combinação de D, M, M' e F. Por exemplo o argumento da oitava linha da tabela A é 2D-M-M', e as contribuições para Sl e Sr são +57066sin(2D-M-M') e -152138cos(2D-M-M'), respectivamente.
Visto as tabelas serem bastante extensas, são apresentados apenas um extracto de cada uma delas:
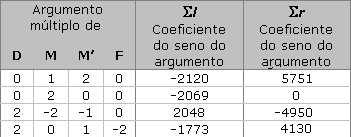
Tabela A
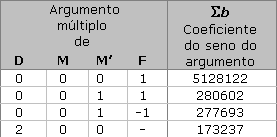
Tabela B
Nota: Na tabela A, a unidade para Sl é 0.000001 graus e 0.001 quilómetros para Sr. Na tabela B a unidade usada para Sb é 0.000001 graus.
No entanto, os termos cujos argumentos contêm o ângulo M dependem da excentricidade da órbita da Terra em torno do Sol, que se encontram actualmente a decrescer com o tempo. Por esta razão, a amplitude destes termos é variável. Para entrar em conta com este efeito multiplicam-se os termos cujos argumentos contêm M ou -M por E, e os que contêm 2M ou -2M por E2, onde:
E = 1 - 0.002516T - 0.0000074T2
O coeficiente, e não o argumento do seno ou do co-seno, deverá ser multiplicado por E. Por exemplo o oitavo termo em longitude é realmente +57066Esin(2D-M-M').
De seguida falta apenas efectuar algumas
correcções. Ou seja, falta adicionar:
|
a Sl: |
+ 3958sinA1 + 1962sin(L'-F) + 318sinA2 |
|
e a Sb: |
- 2235sinL' +382sinA3 +175sin(A1 - F) +175sin(A1 + F) + 127sin(L' - M') - 115sin(L'+M') |
Os termos envolvendo A1 são devidos à acção de Vénus, o termo envolvendo A2 é devido a Júpiter, enquanto que os termos envolvendo L' são devidos ao achatamento da Terra.
![]()
As coordenadas da Lua ficam então:
l = L' + Sl/1000000 (graus)
b = Sb/1000000 (graus)
D = 385000.56 + Sr/1000 (km)
Nota: É necessário dividir as somas por 106 ou por 103 devido às unidades dos coeficientes das tabelas.
![]()
A paralaxe equatorial horizontal da lua, p, poderá então ser obtida através de:
sinp = 6378.14/D