Análise Matemática I - Física, Engª Física, Engª Química, Engª Minas
![]()
![]()
8 de Julho de 1997
Duração: 3 horas
Sem consulta de apontamentos ou textos
Tabela autorizada
Calculadora científica ou gráfica autorizada
1- Seja
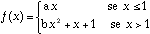
a) Determine
a e b de modo queb) Prove que ![]() é limitada em [-3,5] quaisquer que sejam
é limitada em [-3,5] quaisquer que sejam
c) Determine
a e b de modo que2- Considere a equação diferencial
![]()
a) Determine a solução que verifica ![]() ;
;
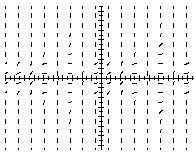
b) Indique, justificando devidamente, se o campo de direcções seguinte pode ser o campo de direcções da equação diferencial dada. (Sugestão: analise os sinais de ![]() )
)
3- Considere as curvas definidas em coordenadas polares por
![]()
a) Esboce a região do plano que é interior a ambas as curvas;
b) Determine os pontos de intersecção das duas curvas;
c) Estabeleça (mas não calcule) os integrais que nos permitem calcular a área da região referida na primeira alínea.
4- Seja
![]()
a) Desenvolva a função f em série de potências de x;
b) Determine o raio de convergência da série obtida;
c) Calcule ![]() .
.
5- Determine a natureza das séries numéricas, dizendo se a convergência é simples ou absoluta,
a) ![]() b)
b) ![]()
6- Duas massas pontuais que se encontram a uma distância fixa atraem-se com uma força que é proporcional ao produto das massas. Supondo que a soma das duas massas é M, quais devem ser as massas individuais de modo que a força de atracção seja tão grande quanto possível? [Quando tiver de determinar extremos deve utilizar o método das derivadas de ordem superior a um.]
7- a) Prove, usando a definição, que se uma função é integrável e é positiva ou nula num intervalo [a,b] o seu integral definido em [a,b] é também positivo ou nulo.
b) Sejam
![]()
as coordenadas paramétricas de uma certa curva. Seja ![]() uma função bijectiva do intervalo
uma função bijectiva do intervalo ![]() no intervalo
no intervalo ![]() . Suponha que, para todo o
. Suponha que, para todo o ![]() do intervalo
do intervalo ![]() se tem
se tem
![]()
Explique que consequências tem este facto sobre o comportamento da curva.
8- Considere a função ![]() definida por
definida por
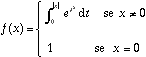
a) Prove que ![]() é par;
é par;
b) Determine ![]() ,
, ![]() ,
, ![]() e
e ![]() ;
;
c) Esboce a curva a partir dos dados obtidos nas alíneas anteriores;
d) Recorrendo às derivadas laterais determine a natureza do extremo local de ![]() no ponto x=0, caso exista.
no ponto x=0, caso exista.