Análise Matemática I - Física, Engª Física, Engª Química, Engª Minas
![]()
![]()
2 de Setembro de 1997
Duração: 3 horas
Sem consulta de apontamentos ou textos
Tabela autorizada
Calculadora científica ou gráfica autorizada
1- Considere a função ![]() definida a partir do gráfico seguinte
definida a partir do gráfico seguinte
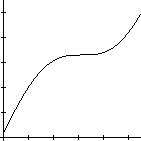
Determine 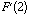 onde
onde 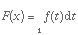 .
.
2- Seja ![]() uma função definida por
uma função definida por
![]()
de domínio ![]() .
.
a) Prove que ![]() é par; b) Determine
é par; b) Determine ![]() ;
;
c) Calcule ![]() ; d) Determine os extremos de
; d) Determine os extremos de ![]() caso existam;
caso existam;
e) Com estes elementos esboce a curva.
3- Seja
![]()
a) Escreva o polinómio de Taylor de grau n para a função ![]() no ponto zero;
no ponto zero;
b) Escreva os respectivos restos de Lagrange e de Taylor-Young;
c) Usando a fórmula de Taylor-Young já obtida, com um valor adequado para n, levante a indeterminação
![]()
4- Os jornais noticiaram no final de Agosto a tentativa de obter a "fusão quente", a fusão de átomos de hidrogénio a temperaturas da ordem dos 3 milhões de graus centígrados. Essas temperaturas são obtidas no acelerador Z do Laboratório Nacional Sandia dos Estados Unidos onde os plasmas são contidos em poderosos campos magnéticos. Nos últimos 10 meses foram obtidas temperaturas que passaram de 300 mil graus centígrados a 1,5 milhões de graus centígrados. O jornalista comentava que "podemos antever que a evolução é exponencial e a fusão nuclear está ao virar da esquina". Supondo que a evolução das temperaturas obtidas é exponencial, indique quando serão obtidas as temperaturas necessárias à "fusão quente".
5- É dado que a série ![]() é convergente se e só se
é convergente se e só se ![]() e que o termo geral da sua sucessão associada é
e que o termo geral da sua sucessão associada é ![]() (se
(se ![]() ).
).
a) Mostre que a soma da série dada é igual a ![]() , se
, se ![]() ;
;
b) A partir da série binomial desenvolva em série de potências de x a função definida por ![]() .
.
c) Se não errou o problema, reencontrou a mesma série ![]() . Porquê?
. Porquê?
6- Calcule o volume gerado pela rotação em torno do eixo dos YY da região plana definida por
![]()
7- Determine a natureza das séries
a) ![]()
b) ![]()
8- a) Prove que entre dois zeros consecutivos da derivada ![]() de uma função derivável
de uma função derivável ![]() há quando muito um zero de
há quando muito um zero de ![]() .
.
b) Considere a curva de coordenadas polares ![]() . Suponha que, para todo o
. Suponha que, para todo o ![]() do intervalo
do intervalo ![]() , se tem
, se tem
![]()
Explique que consequências tem este facto sobre o comportamento da curva.