Análise Matemática I - Física, Engª Física, Engª Química, Engª Geológica, Engª Geográfica, Engª Minas
20 de Junho de 1998
Duração: 3 horas
Sem consulta de apontamentos ou textos
Tabela autorizada
Calculadora científica ou gráfica autorizada
1- Sabe-se que
para todo o x do intervalo ]-1,1[.
a) Quanto vale 
? Porquê?
b) Indique se existe algum ponto de inflexão da função f no ponto x = 0.
c) Indique a fórmula de Taylor-Young de grau p (p ³ 9) para a função f no ponto zero.
2- a) Determine o raio de convergência da série de potências
b) Qual o maior conjunto onde converge a série de potências da alínea anterior?
c) Seja
Diga, justificando, se são verdadeiras ou falsas as seguintes igualdades:
i) 
ii) 
3- Desenvolva em série de potências de x a função F definida por
4- Estude a natureza das séries numéricas:
a) 
b) 
c) 
5- Considere que se pretende fazer passar uma trave de madeira por um corredor em forma de L. Pretende-se saber qual o comprimento máximo da trave que se pode fazer passar pelo corredor
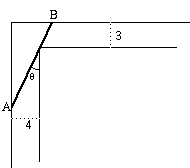
a) Mostre que o comprimento da trave é dado, em função do ângulo
q por
, 
b) Justifique que o comprimento da maior trave que se pode fazer passar pelo corredor é dado pelo valor mínimo de c(
q).c) Determine esse mínimo.
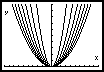
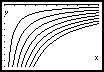
6- Considere as sucessões de funções (de domínio
R) representadas abaixo (os índices da sucessão crescem de cima para baixo de cada figura).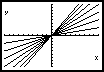
a) Quais parecem convergir pontualmente? Indique qual a função limite.
b) Quais parecem parece convergir uniformemente? Justifique a sua resposta.
7- a) Seja 
uma série de potências. Suponhamos que existe e é diferente de zero
Prove que a série de potências dada converge para todo o x tal que |x| < 1/R.
b) Explique (sem efectuar quaisquer cálculos) como é que a teoria dos desenvolvimentos em série de potências permite resolver equações diferenciais ordinárias de segunda ordem do tipo
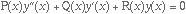
onde P, Q e R são polinómios tais que P(0) > 0.