Sobre
o Movimento e o paradoxo de zenÃo
Eudes Antonio da Costa
UFT/Arraias.
eudes@uft.edu.br
“Um arqueiro está distante
Quantos pontos existem entre o A(0) e o B(2)? Há
infinitos pontos?
Usando do “conceito” de soma dos
infinitos termos da PG podemos “somar” estas parcelas infinitas, sem a
necessidade de um tempo infinito.
A
soma dos infinitos termos da PG (1, 1/2, 1/4, 1/8, 1/16,...
) é 
.
Zenão estava errado em pensar que o movimento era irracional?
1-INTRODUÇÃO
“O que se move deve sempre
alcançar o ponto médio antes do ponto final” (Zenão de Eléia – Os Pensadores)
Alguns Paradoxos têm desafiado e estimulado a razão
humana ao logo dos tempos, entre eles, o Paradoxo de Zenão, filósofo grego de
Eléia. Esse paradoxo é um problema às próprias bases do conhecimento, com
implicações na física e na matemática; é um convite eterno à reflexão; pois a
sua formulação permite-nos pensar sobre o infinito, o tempo, o movimento, o
conhecimento, o número, o contínuo, a reta etc.
2- CONTEXTUALIZAÇÃO
Nossa tentativa será formular/interpretar
este paradoxo matematicamente: geometria euclidiana e por progressões
geométricas (PG), conteúdos do ensino fundamental e médio.
Pretendemos
com isso mostrar que a matemática é, também, uma tentativa de resolução
aos problemas humanos. E ainda, situar o argumento (paradoxo) de Zenão a uma
linguagem matemática do professor/aluno do ensino fundamental e médio.
“Um arqueiro está distante
Faz-se necessário uma discussão da aporia[2]
em sala de aula, para que todos entendam a formulação do aporia e o surgimento
do paradoxo.
3-O
que é um Paradoxo?
Normalmente associamos a paradoxo: aquilo que não tem solução, algo
confuso, algo contrário ao nosso bom-senso,
contrário aos nossos conhecimentos anteriores.
Paradoxo: “Conceito que é ou parece
contrário a comum, contra-senso, disparate, absurdo. Contradição, pelo menos na
aparência” (Dicionário Aurélio, 1988).
Paradoxo: “Afirmação que vai de encontro a
sistemas ou pressupostos que se impuseram, como incontestáveis ao pensamento”
(Abbagnano, 1963)
Paradoxo é uma formulação
reflexiva, da razão, contrária a um sistema ou a um conhecimento tido como
verdadeiro (estabelecido). Logo, um paradoxo parece um absurdo, ou leva-nos a
um absurdo. O paradoxo está na formulação do mesmo, de acordo com uma tese
aceita ou estabelecida e contrária a ela, ou que, aceitando a tese (ou sistema)
chegamos a um absurdo. Surgindo de uma reflexão, o paradoxo origina-se na sua
formulação, na maneira com que foi enunciada; se mudássemos a formulação, já
não se apresentaria como um paradoxo.
No nosso
casso, basta que, afirmássemos que um corpo saindo de A em direção a B deva
sempre percorrer espaços contínuos, por exemplo, avançar sempre dois
centímetros. Isto não nos levaria a uma contradição, bem como não nos
levaria a pensar sobre o infinito, o tempo, o movimento, o conhecimento; outra
maneira de resolver um paradoxo é recorrer a um outro sistema, resolvendo-o tal
como foi enunciado.
Faremos uma
análise desse paradoxo (filosoficamente e matematicamente), procurando
desvanecê-lo, torná-lo claro, apontar soluções (matematicamente), mas não resolvê-lo em definitivo.
4- Os Pitagóricos, Parmênides e Heráclito
Como vimos o
paradoxo nasce na sua formulação. Analisemos o contexto em que Zenão formulou
suas aporias, quais eram os sistemas aceitos, pois o paradoxo é
contrário a estes sistemas, ou o paradoxo se apresentará contrário a
estes sistemas.
Pitágoras de Samos (580/78-497/6
a.C.) é fundador de uma escola “mística”. As idéias pitagóricas apoiavam-se na
multiplicidade e na mudança, e ainda, acreditavam que o sagrado mistério da
ciência tem o seu centro nas matemáticas. Os números são entes (elementos
imutáveis da natureza) e ocupam um lugar. Apregoavam que as coisas[3]
são compostas de números, isto é, feitas de unidades discretas como os pontos;
o número é a essência de todas as coisas. Na Teoria dos números ou teoria da
medida de grandezas eles atribuíam uma dimensão e uma unidade de medida chamada
mônada, para o que eles consideravam ser o menor segmento. Daí um
segmento (finito) pode ser subdividido num número infinito de pequenos
segmentos, cada um deles com um comprimento finito (uma mônada). Para os
Pitagóricos o espaço era composto por pontos e o tempo por instantes, sendo
possível dividir infinitamente, pela teoria das mônadas, com a propriedade de
“continuidade”.
Parmênides
(cerca de 530-
Heráclito (cerca de 450-
5- ZENÃO DE ELÉIA
Zenão de Eléia
(aproximadamente
“Se existe o
menor segmento que mede uma mônada, então podemos tomar dois desses segmentos,
apoiados numa mesma reta e muito próximos um do outro; tão próximo quanto se
queira, porém que não se toquem e deixe entre si um pequeno intervalo. Ora,
como o segmento que mede uma mônada é o menor que existe, então nesse intervalo
cabe um deles (pelo menos) e não esgota o intervalo todo, porque ele é o menor;
e deixa então dois outros intervalos bem pequeninos, nos quais certamente
caberão dois segmentos que medem uma mônada cada (pois a mônada é o menor
segmento); neste caso, essas duas mônadas intercaladas vão deixar quatro
intervalos, nos quais caberão quatro mônadas, que pelo fato não esgotarem cada
intervalo deixarão a seguir oito intervalos... e assim
por diante... “ (PIERRO NETO, 1995)
“a
impossibilidade do movimento é deduzida do fato de que o móvel transportado
deve chegar primeiro à metade antes de alcançar o termo.”
“o mais
lento na corrida jamais será alcançado pelo mais rápido; pois o que persegue
deve sempre começar por
atingir o ponto donde partiu o que foge.” (Os Pré-Socráticos, 1985)
As aporias de
Zenão entravam em conflito com algumas concepções intuitivas sobre o
infinitamente pequeno, bem como, apontava contradições existentes nos conceitos
de movimento, espaço e tempo. Assim nasce o paradoxo.
A problemática
em questão procura invalidar a experiência sensível, embora se apoiando nessa
mesma experiência. Afirma-se a impossibilidade do movimento - da mudança- pois,
por mais próximo que seja o móvel, em um ponto qualquer, sempre terá que atravessar
a metade, depois a metade dessa metade e assim por diante, sem parar, até que
se possa chegar ao ponto desejado que por este caminho seja impossível.
Apesar da
discordância entre a experiência sensível e a aparente força do argumento, o
pensamento de Zenão teve um resultado positivo, pois obrigou a uma nova revisão
crítica de conceitos fundamentais, tais como: o infinito, contínuo, número,
reta, tempo e movimento.
6- A MATEMÁTICA
Euclides de Alexandria (aproximadamente
Euclides
(1944) diz que “ponto é o que não tem partes, ou o que não tem grandeza alguma”
assim admite que ponto seja um ente geométrico primitivo, e não um segmento (o
menor segmento), como admitiam os pitagóricos. No entanto a “sua geometria” não
foi capaz de resolver tal problema, devido a dificuldade em explicar “que uma
reta é composta por infinitos pontos”.
Imaginemos quantos pontos existem entre o A e B.
Euclideanamente entendemos que há infinitos pontos. Dados dois pontos, partindo do ponto A(0) para atingir o ponto B(2), antes temos que atingir C,
ponto médio de AB, e partindo de C para atingir B existe um ponto D, ponto
médio de CB, e assim sucessivamente.
Geometricamente, nunca chegaremos ao ponto B, veja:
saindo do ponto 0 em direção ao ponto 2, temos que primeiro passar pelo ponto 1(metade do espaço 0-2), depois pelo ponto 1/2(metade do
espaço 1-2), 1/4(metade...), 1/8 (metade...), 1/16(metade...).
Veja que 
, 
, 
, 
, 
,... , e
assim temos
, 
, 
, 
, 
. E assim, infinitamente, seja qual for o espaço a mais
percorrido, sempre será menor que 2. Precisaríamos de um tempo infinito para
realizar esta soma, o que é impossível, por este método. Este fato mostra a
dificuldade em explicar na Geometria Euclidiana (e utilizar em eventos físicos,
tais como o movimento e o tempo), que uma reta é ‘composta’ por infinitos
pontos.
Agora, usando do “conceito” de somas
dos infinitos termos[4]
de progressões geométricas podemos somar
matematicamente estas parcelas infinitas, sem a necessidade de um tempo
infinito.
Calculemos a soma dos infinitos termos da PG (1, 1/2,
1/4, 1/8, 1/16,...), sendo 
, 
e sabendo que a soma
dos infinitos termos dessa PG é 
temos .
Ou ainda, faça 
e multiplique ambos os membros da equação por 2,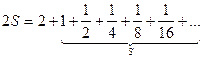 
ou 
e
.
Mesmo que as distâncias fossem sendo diminuídas, haveria
uma infinidade de pequenos trechos a serem cobertos e eles jamais chegaria ao objetivo. O paradoxo pressupunha que a soma de
uma infinidade de pequenas distâncias deveria ser infinita (ou que o tempo de
percurso seria infinito) e aí está o erro. Quando descobriram séries infinitas
cujas somas convergem para valores finitos, o paradoxo perdeu a força, pois não
é necessário um tempo infinito para realizar a soma de infinitas parcelas.
“o desenvolvimento
de noções relacionadas com infinitésimos e infinitos e processos somatórios que
só foram esclarecidos de vez com a invenção do cálculo nos tempos modernos. Os
paradoxos de Zenão, (...) inserem-se nesta (...) linha
de desenvolvimento”. ( Eves, 2004)
7- CONSIDERAÇÕES FINAIS
Hoje, usando da matemática temos condições de mostrar que
Zenão estava errado em pensar que o movimento era irracional a partir das
aporias. E estas aporias conduziram a absurdos que, por vários séculos, levaram
a afirmar que aceitos os sistemas heracliteano e pitagórico as aporias
conduziam a um paradoxo ( sem solução). No entanto,
basta recorrer a outros sistemas, no caso o matemático, para se encontrar tal
solução. Não queremos negar a importância que Zenão teve (e tem) em formular
tais aporias; pretendemos apenas elucidar a importância que teve seus
paradoxos; sem dúvida, Zenão é um personagem ímpar na história e na
consolidação do pensamento ocidental, pois foram tais aporias que possibilitou
pensar melhor o movimento, o infinito etc.
Como o
paradoxo nega contradições intuitivas, comum ainda hoje na maioria dos nossos
alunos, a leitura e a discussão do mesmo tem um aspecto positivo, fazem com que
os alunos percebam algumas contradições em seus argumentos.
Trabalhando com alguns paradoxos nas aulas de matemática
percebi que alunos deixaram de ver a matemática como algo mágico e sem
utilidade (matemágica). Reforço sempre que a matemática é a uma forma histórica
de resolver problemas humanos, isto é, a matemática é algo necessário e
concreto e não desvinculado da realidade, como pensa a maioria dos alunos. Com
isso tento tornar a matemática mais atrativa para os alunos.
“A matemática é uma grande aventura nas
idéias; a sua história reflete alguns dos mais nobres pensamentos de inúmeras gerações.” (Struik, 1992).
8- REFERÊNCIAS
BIBLIOGRÁFICAS
1-
ABBAGNANO, Nicola. DICIONÁRIO DE FILOSOFIA.
Fundo
de cultura econômica. México. 1963.
2-
ÁVILA, Geraldo. AS SÉRIES INFINITAS. In:
REVISTA DO PROFESSOR DE MATEMÁTICA - 3O. SBM. São Paulo. 1996.
3-
Boyer, Carl B. História da matemática. São Paulo. 1974.
4-
Euclides. elementos de geometria. Série Científica. Edições Cultura. São Paulo. 1944.
5-
EVES, Howard. INTRODUÇÃO À HISTÓRIA DA MATEMÁTICA. Editora da Unicamp.
Campinas-SP. 2004.
6-
FERREIRA, Aurélio Buarque de Holanda. NOVO DICIONÁRIO DA
LÍNGUA PORTUGUESA. (1º edição, 10º impressão) Editora Nova Fronteira. Rio
de Janeiro. 1988.
7-
OS PRÉ-SOCRÁTICOS. Coleção Os Pensadores. 2
ed. Abril Cultural. São Paulo. 1976.
8-
Pierro Netto, Scipione
di. Matemática Conceitos e Histórias. 8ª série.
Editora Scipione. São Paulo. 1995.
9-
Struik, Dirk J. A história concisa das
matemáticas. Gradiva. Lisboa- Portugal. 1992.