

As deslocações são apoiadas pelo programa
E pelo "Programa para Escolas" da FCTUC. Para calendarização de palestras nas escolas básicas e secundárias
contactar
| Palestra |
Resumo |
|
“Números Astronómicos” |
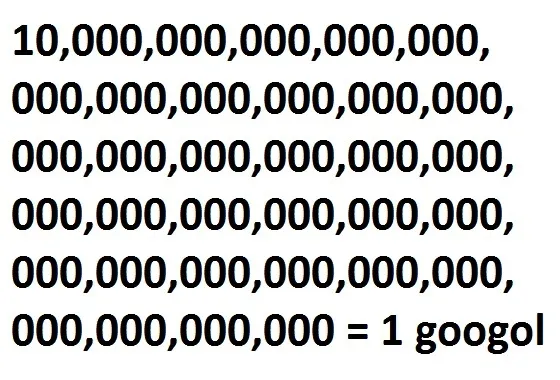 |
Existem números muito grandes, frequentemente relacionados com a Astronomia (Ciência que estuda a posição, os movimentos e a constituição dos corpos celestes) e por isso são chamados "números astronómicos". Nesta palestra serão mencionados e comparados vários números da Astronomia e como Arquimedes contou quantos grãos de areia haverá no Universo. Será referida a Unidade Astronómica e os números Googol e Googolplex e terminaremos com o problema da construção de uma ponte entre a Terra e a Lua usando apenas papel vegetal. Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Básico. Material: um videoprojetor (uso o meu próprio computador) |
“A Matemática e as mensagens secretas” |
|
Com a Criptografia, uma área da Matemática, podemos esconder ("codificar" ou "encriptar") os conteúdos das nossas mensagens de modo a que pessoas não autorizadas não as consigam entender (a não ser que sejam mesmo muito, muito inteligentes!). Nesta palestra, iremos trabalhar alguns exemplos simples de Criptografia, usando métodos com mais de 2000 anos como o do imperador romano Júlio César e usando métodos mais recentes como o da máquina ENIGMA, utilizada na II Guerra Mundial, ou o do software de codificação conhecido por PGP ("Pretty good privacy", isto é "Privacidade bastante boa"). Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Básico ou do Ensino Secundário. Material: um videoprojetor (uso o meu próprio computador) |
“Episódios interessantes e curiosos da História da Matemática em Portugal” |
 |
A História da Matemática em Portugal está recheada de episódios curiosos que poderão interessar um público alargado de estudantes, professores e público em geral. Desde a famosa curva loxodrómica de Pedro Nunes, até à demolição do Observatório Astronómico da Universidade de Coimbra, desde os obstáculos ao reconhecimento do trabalho de Daniel da Silva até à criação do primeiro clube escolar de Matemática em Portugal, desde a prisão de Anastácio da Cunha pela Inquisição até ao modo como Gomes Teixeira escolheu o curso de Matemática, muitas (pequenas) histórias ajudam a conhecer melhor os matemáticos da nossa história e fornecem uma perspetiva humanizada sobre os que fizeram Matemática em Portugal. Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Básico ou do Ensino Secundário Material: um videoprojetor (uso o meu próprio computador) |
"A Matemática está em toda a parte, também na Música Pop e Rock” |
  |
"A Matemática está em toda a parte, também na Música Pop e Rock” Tal como proclamou a UNESCO em 2020, a Matemática está em toda a parte! Com efeito, o primeiro Dia Internacional da Matemática, celebrado a 13 de março desse ano, proclamou essa ideia ("Mathematics is Everywhere”). E tem toda a razão, embora muitas relações, talvez por serem inesperadas, não revelem tão facilmente a Matemática. A música Pop e a música Rock têm mais a ver com a Matemática do que muitos pensam. Muitos grupos musicais vão procurar inspiração em temas matemáticos como os Tool ou os Blue Man Group (estes últimos deram em 2020 uma série de concertos em Portugal de 28 de maio a 7 de junho). Outros grupos glosam temas matemáticos (a sucessão de Fibonacci, a banda de Moebius, o número PI, o número de Ouro, o infinito, os fractais) nas suas músicas e outros escolhem mesmo nomes matemáticos como "MuteMath", “Moebius Band” ou “InfinitY Minus Zero”. Há um estilo de música conhecido como “Math Rock” onde são usadas relações numéricas mais ou menos complexas para construir a música, com grupos como os Don Cabarello, 65daysofstatic, Upsilon Acrux, 31Knots, Giraffes? Giraffes!, Converge ou The Number Twelve Looks Like You. Até existe em Inglaterra um festival anual de Rock Matemático intitulado ArcTanGent (@ATGFestival) que em 2023 decorre na cidade de Bristol de 16 a 19 de agosto. Vários grupos portugueses procuram inspiração na Matemática como os GNR (com “Dama ou Tigre”) ou os Santos e Pecadores (com “O último zero do cem”). Nem sempre a visão expressa é favorável à Matemática pois alguns grupos usam as suas músicas para exprimir a sua frustração com a Matemática, como os White Stripes (com “Black Math”) ou Jimmy Buffet (com “Math Sucks”). Nesta conferência iremos ver, com música e vídeos, um pouco da actividade de alguns dos cantores e gruposPop e Rock relacionada com a Matemática. Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Básico ou do Ensino Secundário Material: um videoprojetor (uso o meu próprio computador) e ligação a um sistema sonoro com alguma qualidade (para ligar ao computador para se ouvirem algumas das músicas e videos que mostrarei); é indispensável que o som seja bem ouvido na sala, pelo que colunas portáteis ligadas diretamente ao computador não serão suficientes. |
“O conto do vigário, Fernando Pessoa e a Matemática” |
 |
A expressão "Conto do Vigário" aparece frequentemente nas páginas dos jornais. Segundo Fernando Pessoa a origem do Conto do Vigário está nas aventuras e desventuras de Manuel Peres Vigário, um pequeno lavrador e negociante de gado, que há muitos anos viveu algures, num concelho do Ribatejo. Um dia Manuel Peres Vigário tropeçou num fabricante ilegal de notas falsas e viu-se em muitos maus lençóis! Infelizmente a atividade dos falsários, farsantes e outros embusteiros baseia-se muito na ignorância das pessoas mas também na cupidez que as torna descuidadas e presas fáceis de quem domina a psicologia humana de forma hábil. Podemos apontar muitos exemplos, tanto em Portugal (a começar pela famosa Dona Branca) como no estrangeiro (de que o caso retumbante mais recente foi Bernard Madoff, com uma fraude avaliada em 65 mil milhões de dólares). A eficácia do "Conto do Vigário" também se baseia na ignorância do que é realmente o crescimento exponencial e o que está por detrás do chamado esquema em pirâmide (também conhecido como esquema de Ponzi). Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Básico ou do Ensino Secundário Material: um videoprojetor (uso o meu próprio computador) e ligação a um sistema sonoro com alguma qualidade (para ligar ao computador para se ouvirem alguns videos que mostrarei) |
“Como a Matemática Ajudou os Aliados a Ganharem a Segunda Guerra Mundial” |
 |
Actualmente todos reconhecem que a Matemática está presente em todas as áreas da actividade humana, mas poucos conhecem efectivamente a Matemática que está presente em muitas dessas áreas. A Arte da Guerra é também uma grande consumidora de Matemática o que aliás levanta questões éticas interessantes sobre a responsabilidade social dos matemáticos (e dos professores de Matemática). Esta sessão vai-se debruçar sobre um dos períodos mais trágicos da História da Humanidade, a II Guerra Mundial, que decorreu entre 1939 e 1945 e provocou a morte de milhões de pessoas. Muita da Matemática então utilizada só foi divulgada muitos anos mais tarde, sobretudo por razões de segurança. Hoje pode-se fazer um balanço bastante detalhado dessa utilização. Serão passados em revista temas como: as mulheres "computadoras" e o aparecimentos dos primeiros computadores, os códigos secretos e o papel do matemático Alan Turing, a programação linear e o matemático George Dantzig, as cónicas e a detecção da rota dos "invisíveis" submarinos inimigos. Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Básico ou do Ensino Secundário Material: um videoprojetor (uso o meu próprio computador) e ligação a um sistema sonoro com alguma qualidade (para ligar ao computador para se ouvirem alguns videos que mostrarei) |
“Gráficos enganadores como os reconhecer, como os evitar” |

By Joxemai - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=18603789 |
No livro “Como mentir com a Estatística” o autor Darrell Huff já há mais de 60 anos alertava que “médias e relações e tendências e gráficos nem sempre são o que parecem”. Os gráficos podem ser usados para melhor transmitir uma ideia importante mas podem também servir para puxar o sensacionalismo, aumentar desproporcionadamente o impacto, confundir o leitor ou simplificar demasiado as questões. Os gráficos são usados desde há milhares de anos em diferentes contextos e com objetivos diferentes, desde a medição da altura das águas do Rio Nilo até ao uso do gráficos no século XIX por Florence Nightingale para obter do governo inglês de então uma melhoria das condições sanitárias nos hospitais, passando pelo célebre gráfico da Campanha de Napoleão na Rússia (1812-1813) ou pelos gráficos que o bispo Nicole Oresme traçou no século XIV para descrever o movimento dos corpos. Estamos numa sociedade em que a informação nos é apresentada repetida e insistentemente. Com uma informação galopante a sua representação em termos de gráficos pode ser uma ajuda muito eficaz ou … um autêntico embuste. Poderemos classificar os possíveis gráficos enganadores em várias categorias de que destaco duas: 1-Gráficos com um eixo dos YY truncado, 2-Proporcionalidade de áreas errada. Teremos de usar gráficos para melhor apresentar certas ideias, mas precisamos de ter cuidado com o modo como os usamos para não deturpar a ideia que queremos apresentar. Por fim, como cidadãos informados e críticos, teremos de saber analisar se os gráficos que nos são apresentados são fiáveis e corretos. Duração: 90 minutos Público-alvo: Alunos do Ensino Básico ou do Ensino Secundário. Material: um videoprojetor (uso o meu próprio computador) |
“A Matemática na Exploração Espacial” |

By Johannes Kepler - Johannes Kepler: Mysterium Cosmographicum, Tübingen 1596, Tabula III: Orbium planetarum dimensiones, et distantias per quinque regularia corpora geometrica exhibens., Public Domain, https://commons.wikimedia.org/w/index.php?curid=37300 |
A Astronomia é uma das áreas da Matemática Aplicada com uma história mais antiga e mais rica. Hoje a exploração espacial é uma área considerada das mais importantes e mobiliza cada vez mais conhecimentos matemáticos. Serão passados em revista alguns dos exemplos da conquista espacial moderna. Veremos algumas contribuições para a evolução espacial de matemáticos mais conhecidos como Galileu, Kepler ou Gauss, mas também as de personagens menos conhecidas como Katherine Johnson (cujo trabalho é retratado no filme "Hidden Figures”). Iremos conhecer dois matemáticos portugueses com uma contribuição notável para a Astronomia: Pedro Nunes e Monteiro da Rocha. Também serão referidas outras contribuições da Matemática para a Exploração Espacial e alguns desastres devido a erros matemáticos (caso do "Mars Climate Orbiter” e do primeiro lançamento do foguetão Ariane 5). Por fim serão referidas as indústrias portuguesas ligadas ao espaço e a iniciativa da Agência Espacial Europeia-ESA que é gerida em Portugal pelo Instituto Pedro Nunes, criado por iniciativa da Universidade de Coimbra em 1991. Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Básico ou Secundário. Material: um videoprojetor (uso o meu próprio computador) e um sistema sonoro ligado ao computador (podem ser colunas portáteis). |
“Uma competição internacional de Modelação Matemática para o Ensino Secundário” |

|
Equipas portuguesas já obtiveram três Menções Honrosas numa competição internacional de Modelação Matemática destinada a estudantes do Ensino Secundário, a IM2C - International Mathematical Modeling Challenge. Esta competição é organizada anualmente pelo COMAP - Consórcio para a Matemática e Suas Aplicações: http://www.immchallenge.org/ Esta competição internacional é aberta a todos os países, sendo que só podem ser submetidas soluções de duas equipas de cada País. Têm participado mais de trinta países. O objetivo do IM2C é promover o ensino da modelação matemática e aplicações. O IM2C incentiva alunos e professores a experimentar o poder da matemática para ajudar a entender, analisar e resolver problemas do mundo real fora da própria matemática – e fazê-lo em contextos muito realistas. Esta competição internacional é disputada por equipas do Ensino não superior, constituída por 4 alunos e um professor. Durante 5 dias seguidos os alunos trabalham na solução do problema proposto em cada ano com acesso a todo o tipo de recursos, incluindo calculadoras, computadores, bibliotecas e internet. Têm de produzir uma solução com o máximo de 20 páginas, que inclui sempre uma carta de uma página a defender perante alguma entidade o valor da solução proposta. Iremos ver que problemas já foram propostos em anos anteriores e algumas das soluções propostas por alunos. Duração: 50 ou 90 minutos Público-alvo: Alunos do Ensino Secundário. Material: um videoprojetor (uso o meu próprio computador) e um sistema sonoro ligado ao computador (podem ser colunas portáteis). |
Autor: Página científica pessoal
![]() Departmento de Matemática da Universidade de Coimbra
Departmento de Matemática da Universidade de Coimbra