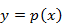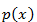Matemática no Ocidente Europeu
Evolução da Álgebra
Os primeiros a dispor de um método para obter as soluções
das equações do segundo grau foram os babilónios. Os árabes, com
a panóplia de informação de diferentes civilizações, evoluíram
no rigor e no tratamento de equações do 2º e do 3º grau. Em
1202, Leonardo de Pisa,
mais conhecido por
Fibonacci, durante o seu contacto com as diferentes
civilizações publicou a obra
Liber Abaci. As obras
de Fibonacci abriram portas para a álgebra na Itália da
Renascença. No séc. XV
Luca Pacioli, embora não tenha feito progressos na álgebra,
cria o famoso número de
ouro e tenta tornar a escrita retórica (palavras) numa
escrita sincopada (abreviações).
Por exemplo: A equação
Cem anos depois Nicolo Tartaglia encontra um método para
calcular equações do 3º grau do tipo
O autor do método para determinar a solução de uma
equação do 4º grau foi
Ludovico Ferrari. Este matemático, usando o conhecimento de
Bhaskara, transforma uma equação de grau 4 numa equação de grau
3 de onde são conhecidos todos os métodos para obter as suas
soluções. Com Ferrari,
os métodos para determinar estas equações estavam terminados, no
entanto, a notação que facilita a leitura de documentos evoluiu
muito lentamente. Neste campo destacam-se Nicolau de
Oresme
(séc. XVI) com notações para frações; Viète (séc. XVII) com
notações para incógnitas; Descartes com a classificação das
equações pelo grau.
Das Equações à Álgebra Moderna Na sequência do trabalho dos algebristas italianos e da emancipação da geometria na álgebra, houve muitos matemáticos a tentar a sua sorte na resolução de equações. O alemão Tschirnhaus (em 1683) sugere um método para determinar raízes da equação polinomial 
O método consiste em saber fazer, convenientemente, uma
mudança de incógnita do tipo
Deve-se a Évariste
Galois (séc XIX) a demonstração da impossibilidade de
existir fórmula resolvente para o 5º grau e grau superior. Este
matemático reúne o trabalho de matemáticos anteriores, inclusive
Gauss e Abel, e cria a Teoria de Grupos/Corpos. Esta teoria
mostrou-se ser importante e fundamental nas áreas de Teoria dos
Números, Geometria e Álgebra.
As famosas
questões das construções geométricas da Grécia Antiga são
facilmente respondidas usando Corpos e suas dimensões.
Outras
geométricas
Nos Elementos de Euclides existe uma definição que levou
muitos matemáticos a tentar provar a sua veracidade. Essa
definição é o 5º postulado.
No livro I dos Elementos existem proposições que dependem
do postulado das paralelas, elas são a proposição I, 17 e as
proposições depois da 28 com a exceção da 31. Assim, todas as
outras são independentes, como as que indicam o caso das
congruências de triângulos.
Os primeiros a tentar provar, com algum rigor, o 5º
postulado foram os árabes
Ign al-Haytham e Omar
Khayyam usando o método de redução ao absurdo. Mais tarde
John Wallis substitui o 5º postulado por outra definição e prova
o postulado das paralelas. Infelizmente a definição que usou é
equivalente ao postulado, logo a sua prova não é válida.
Saccheri (séc. XVII)
pegou no quadrilátero de Omar e quando tentou provar, por
redução ao absurdo, o 5º postulado chegou a conclusões válidas
num outro “universo” mas, desistiu de tudo o que descobriu por
ser “algo que repugna a
Natureza”. Johann Lambert, Adrien Legendre e John Playfair
construíram outras proposições independentes do 5º postulado e
notaram que a “visualização” dessas proposições era possível
numa “Superfície Esférica Imaginária”. No séc. XIX,
Schweikart e Taurinus
provaram que de facto era possível construir estas proposições
usando propriedades esféricas imaginárias.
Carl Gauss,
Johann Bolyai e o
russo Lobatschewski
criaram a geometria hiperbólica (séc XIX). Gauss foi o 1º a
descobrir a nova geometria, no entanto, não a publicou com medo
das críticas dos incultos. O filho do seu amigo, Johann Bolyai,
também descobriu esta nova geometria e sem receio publicou-a.
Mais tarde, Lobatschewski
demonstra com mais rigor e simplicidade a geometria hiperbólica,
no entanto, esta nova descoberta só ganhou poder em 1867 com a
publicação de um trabalho de
Bernhard Riemann.
Riemann com a distinção entre ilimitado e infinito, criou
a geometria elíptica.
Esta geometria é construída numa superfície esférica onde
facilmente se verifica que um quadrilátero pode ter a soma dos
ângulos internos superior a
Para interpretar os conceitos primitivos no qual os
axiomas transformam-se em proposições verdadeiras usam-se
modelos.
Eugenio Beltrami
criou o modelo da
Pseudo-Esfera
onde as curvas (retas da geometria hiperbólica) verificam
praticamente todas as proposições da geometria hiperbólica. Para
facilitar esta visualização ainda criou o “mapa de Beltrami”
onde as curvas transformam-se em retas.
A aceitação das novas geometrias criou um enorme impacto
em todas as áreas do saber. As questões que se levantaram
incidiam na consistência da axiomática dos Elementos de
Euclides.
Para combater este problema, o matemático
Hilbert constrói os
novos Fundamentos de
Euclides. Começa por introduzir conceitos primitivos, de
seguida diz que todos os axiomas são independentes uns dos
outros, por último prova que “se a geometria euclidiana é
consistente então a Aritmética também o é”. A demonstração de
consistências entre as geometrias foi reduzida a nada quando
Gödel, em 1931,
mostra que “ não é possível provar a consistência duma teoria
dedutiva dentro da própria teoria”.
|



OCIDENTE EUROPEU
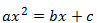
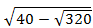
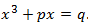



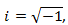 e suas
regras operatórias, conseguindo assim resolver todas as equações
do 2º e 3º grau. Em Portugal, Pedro Nunes pega nas obras de
Tartaglia-Cardano e cria uma álgebra com um maior rigor,
perfeição e clareza de exposição.
e suas
regras operatórias, conseguindo assim resolver todas as equações
do 2º e 3º grau. Em Portugal, Pedro Nunes pega nas obras de
Tartaglia-Cardano e cria uma álgebra com um maior rigor,
perfeição e clareza de exposição.