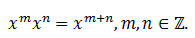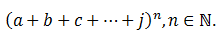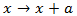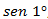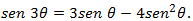Matemática na Civilização Islâmica

A importância da tradução

         O povo islâmico, mais propriamente os Califas, deram uma grande contribuição para todo o mundo. Estes profetas de Maomé, devido ao enriquecimento de várias culturas, construíram “bibliotecas” onde traduziram para árabe todas as obras científicas gregas, persas, hindus e da Mesopotâmia. Mais tarde, com a construção de escolas de tradutores, a Europa conseguiu converter de árabe para latim as obras deixadas pelos Califas.

Al-Khwarizmi

        O povo islâmico tinha várias maneiras de representar os números, mas foi Al-Khwarizmi (séc. IX d.C.), o primeiro matemático a usar e a escrever o sistema decimal dos hindus, exceto no tratamento de frações. Este matemático trabalhou na Casa da Sabedoria, em Bagdad, importante academia dotada de uma Biblioteca e Observatório Astronómico e deixou obras de Aritmética, Álgebra, Astronomia, Geografia e o Calendário.

         Na Aritmética, este matemático dá as bases para o cálculo, usa algoritmos operacionais bastante semelhantes aos nossos e afirma que todos os números podem ser representados pelo sistema decimal hindu. As frações decimais foram primeiramente usados por al-Uqlidisi (952 d.C.), sistematicamente usadas por as-Samaw’al (1174) e foram explicadas como “as frações mais simples para qualquer tipo de cálculo” pelo persa Al-Kashi (1427). É nesta época que pode dizer-se que o sistema decimal posicional está completo.

         Na álgebra, Al-Khwarizmi ensina técnicas de resolução de equações, usando processos semelhantes aos babilónicos e aos gregos, classifica os diferentes tipos de equações e reconhece que uma equação quadrática pode ter duas raízes positivas, uma única raiz ou ser impossível. Al-Karagi, matemático islâmico, também contribuiu para o desenvolvimento da álgebra, onde mostrou que

e usou a demonstração por indução nas suas provas. Onde este matemático “falhou”, as-Samaw’al conseguiu superar, nomeadamente nas “regras dos sinais” para operacionalizar em polinómios e no conceito de expoente nulo.

Também provou que

            Este matemático árabe brilhou no tratamento das equações até ao 3ºgrau, tentou demonstrar o 5º Postulado por redução ao absurdo, definiu uma teoria de proporções e conseguia extrair raízes de índice superior através do desenvolvimento do binómio

           Na tentativa de demonstrar o Postulado das Paralelas, considerou um quadrilátero [] , com os dois ângulos base A e B retos e os dois lados laterais AD e BC congruentes. É facilmente provado que os ângulos C e D são iguais sem invocar o 5º postulado. Usando a congruência dos triângulos [ABC]  e [ABD] , para provar que as diagonais do quadrilátero são iguais, de seguida, usar novamente a congruência dos novos triângulos [ACD]  e [BCD] , assim, os ângulos C e D são iguais. Para provar que os ângulos C e D são retos, Omar por redução ao absurdo concluiu que não podiam ser nem agudos nem obtusos, no entanto invocou uma proposição equivalente ao 5º postulado deitando abaixo toda a sua tentativa.
          Na álgebra este árabe resolvia os problemas com bastante rigor e mostrou que nas equações cúbicas era possível encontrar soluções usando secções cónicas. Também nesta área houve outros matemáticos que fizeram grandes avanços importantes como é o caso de Sharaf al-Din al-Tusi. Através da simplificação de equações, aplicando ou o artificio  e  ou fazendo divisões por binómios.

         Na área da trigonometria, os islâmicos pegaram nas cordas de Ptolomeu, nos conceitos de senos e cosseno e criaram a tangente, a cotangente, a secante e cossecante. Determinaram a lei dos senos, a fórmula para o seno da soma e da diferença e produziram tábuas trigonométricas, no sentido de poderem construir triângulos esféricos para encontrar Meca. Um dos maiores desafios no campo da Astronomia era encontrar, com muita precisão, , para isso, os islâmicos formularam

.