Vamos trabalhar com Sucessões Convergentes e Divergentes

           Usando a apliqueta em baixo e deixando-a carregar, vamos estudar a sucessão cujo termo geral é dado por,

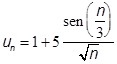
Que parece convergir para L=1. Movimentando o cursor ε pode-se aumentar ou diminuir e assim controlar a largura da faixa horizontal que está no eixo dos YY’s entre os valores L - ε e L + ε. Se se movimentar o cursor N, controlamos a faixa vertical ilimitada traçada para valores de abcissa maiores do que o valor N.

Assim, para a sucessão já definida pode-se dizer que, para todo o ε positivo e próximo de zero, existe sempre um valor de N a partir de uma certa ordem que para todos os elementos da sucessão estão entre os valores L - ε e L + ε para L=1.

Para se observar mais pontos de abcissa do gráfico basta clicar o rato ao mesmo tempo que se carrega na tecla SHIFT (do teclado) e consegue-se então ver os pontos do gráfico até à abcissa 300.

Agora que já sabem todas as regras vamos exercitar:

Limites e Convergências

O limite da seqüência (a_n) L é se dado qualquer ε>0, para um N>0 tal que |a_n-L|<ε para todos os n≥N.

A faixa amarela é L ± ε e as correspons região azul aos n ≥ N. Os pontos verdes são dentro ε de L e os pontos vermelhos e vermelho x não são. O limite é de L se por qualquer ε dada tem de ser capaz de mover a região azul suficientemente longe para a direita que não existem X vermelho.

This is a Java Applet created using GeoGebra from www.geogebra.org - it looks like you don't have Java installed, please go to www.java.com

Use os controles deslizantes para alterar os valores de ε e N.

Sucessão: (a variável de indexação deve ser n)
Limite Proposto: L=

Nota: botão direito do mouse na região branca para ampliar ou reduzir ou alterar a escala dos eixos. Desvio à esquerda, clique e arraste para mover os eixos.

Created by David Richeson using GeoGebra.

1. Muda agora L para L=2. O que é que acontece? O que podes concluir, a sucessão converge ou não para L=2?

2. Muda agora o valor de L para L=0. Explica também se a sucessão converge ou não.

3. Experimenta agora fazer o mesmo estudo para a sucessão,

4. DESAFIO: Muda agora a expressão da sucessão faz o mesmo estudo para a nova sucessão o que verificas?

NOTA: Se não tiveres nenhuma ideia de outra sucessão usa a sucessão com termo geral:

Esta sucessão será convergente?