Trabalho
número 3: Resolução de uma questão de exame
Questão 4 do Grupo I da 2ª fase de
Matemática de 2011
Na figura $1$, está
representada, num referencial o.n. $xOy$, parte do gráfico de uma
função polinomial $f$ de grau 4.
Qual das expressões
seguintes pode definir a função $f''$, segunda derivada de $f$?
(A)
$(x-3)^2$ (B)
$(x+3)^2$ (C) $9-x^2$ (D)
$x^2-9$
Resposta:
Para responder a esta
questão precisamos estudar a função f:
- O domínio de $f$ é $\mathbb{R}$;
- A função $f$ é contínua;
- Pontos de interseção com os eixos coordenados:
- A função
tem dois zeros da função, isto é, existe um $x_0<0$ e um
$x_1>0$ tal que $f(x)=0$;
- $f(0)<0$;
- Intervalos de monotonia e existência de extremos:
- Como $f$ é decrescente em $]-\infty,x_2[$ e em $]0,x_3[$,
podemos concluir que, nestes intervalos, a derivada de $f$,
$f'$ é não positiva, sendo nula em $x_2$ e $0$, isto é,
$f'(x_2)=f'(0)=0$;
- Como $f$ é crescente em $]x_2, 0[$ e em $]x_3, +\infty[$,
podemos concluir que, nestes intervalos, a derivada de $f$,
$f'$ é não negativa, sendo nula em $0$ e $x_3$, isto é,
$f'(0)=f'(x_3)=0$;
- Sentido das concavidades e pontos de inflexão:
$x$
|
|
$x_0$
|
|
$x_2$
|
|
$0$
|
|
$x_3$
|
|
$x_1$
|
|
$f$
|
$\bigcup$ |
0
|
$\bigcup$ |
ponto de inflexão
|
$\bigcap$
|
$<0$
|
$\bigcap$
|
ponto de inflexão |
$\bigcup$ |
0
|
$\bigcup$ |
$f''$
|
+
|
|
+
|
0
|
-
|
|
-
|
0
|
+
|
|
+
|
A partir desta tabela, concluímos que $f''(0)<0$.
Na tabela que se segue, podemos visualizar o gráfico das quatro
opções dadas, assim como o valor que tomam no ponto zero:
Opções
|
Gráfico
|
Sinal de $f''(0)$
|
(A) $(x-3)^2$
|

|
$f''(0)=9>0$ |
(B) $(x+3)^2$ |
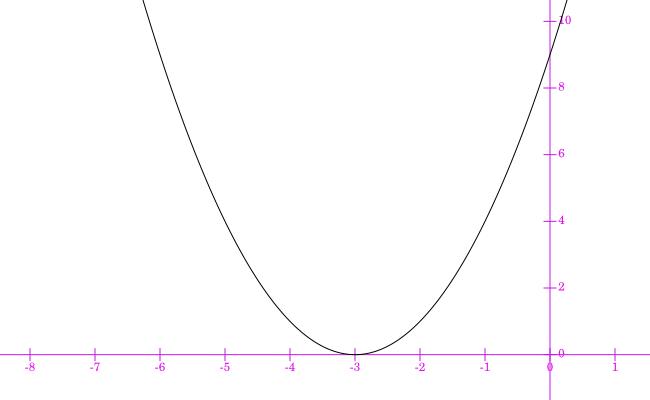
|
$f''(0)=9>0$
|
(C) $9-x^2$ |

|
$f''(0)=9>0$ |
(D) $x^2-9$ |
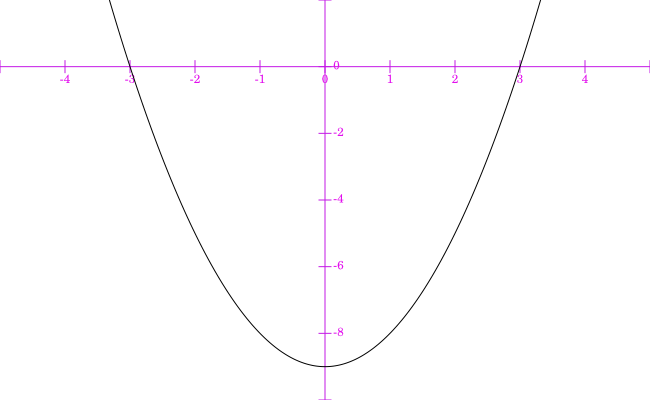
|
$f''(0)= -9<0$
|
Pelo que a única opção correta é a alínea (D)
$x^2-9$.



