

Leonardo Fibonacci,
também conhecido como Leonardo de Pisa, Leonardo
Pisano ou ainda Leonardo Bigollo, (Pisa,
c. 1170
— Pisa?, c. 1250)
mas, na maioria das vezes, simplesmente como Fibonacci
foi um matemático italiano,
tido como o primeiro grande matemático europeu do
Medievo.
É considerado por alguns como o mais talentoso
matemático ocidental da Idade Média.
Ficou conhecido pela descoberta da sequência de
Fibonacci e pelo seu papel na
introdução dos algarismos arábicos na Europa.
Com outros matemáticos do seu
tempo, contribuiu para o renascimento das ciências
exactas,
após a decadência do último
período da antiguidade clássica e do
início da Idade Média, mas Fibonacci
destacou-se ao escrever o Liber Abaci, em 1202
(actualizado em 1254),
a primeira obra importante sobre matemática desde
Eratóstenes,
isto é, mais de mil anos antes. O Liber Abaci
introduziu os numerias hindu-arábicos na Europa,
além de discutir muitos problemas
matemáticos.
Fibonacci é
também conhecido pela sequência numérica
nomeada após sua morte como sequência de Fibonacci.
Ele não descobriu, mas usou-a como exemplo no Liber Abaci.
SEQUÊNCIA DE FIBONACCI
Na matemática, os números de Fibonacci são os números que compõe a seguinte sucessão de números inteiros.
Em termos matemáticos, a sequência é definida recursivamente pela fórmula abaixo:
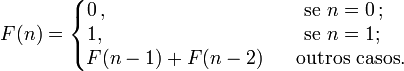
A sequência de Fibonacci tem
aplicações na análise de mercados financeiros,
na ciência
da computação e na teoria de jogos.
Também aparece em configurações biológicas,
como, por exemplo, na disposição dos galhos
das árvores ou das folhas em uma haste, no arranjo do
cone da alcachofra, do abacaxi, ou no desenrolar da
samambaia.
Origem: Wikipédia, a enciclopédia livre.
Os
números de Fibonacci ligam-se facilmente à
natureza. É possível encontrá-los no
arranjo das folhas do ramo de uma planta, nas copas das
árvores ou até mesmo no número de
pétalas das flores. Podemos também encontrar a
espiral de Fibonacci nas sementes das flores, em frutos e
pinhas.
Espirais
de Fibonacci nas sementes das flores de um
girassol:
Os números de Fibonacci podem ser encontrados na organização das sementes na coroa das flores.
As sementes parecem formar espirais a curvar tanto para a direita como para a esquerda. Se contar as espirais perto do centro nas duas direcções, serão ambos números de Fibonacci.
Espirais de Fibonacci nas pinhas:
Da mesma forma, o número de espirais de Fibonacci pode ser encontrado frequentemente em muitas outras formas vegetais como sejam: as folhas das cabeças das alfaces, a couve-flor, as camadas das cebolas ou os padrões de saliências dos ananases e da pinhas, como se pode ver nesta figura.

 Consegue contar o
número de espirais vermelhas e verdes, os números
encontrados são familiares?
Consegue contar o
número de espirais vermelhas e verdes, os números
encontrados são familiares?As ramificações e os números de Fibonacci:
Uma planta em particular, mostra os números da sucessão de Fibonacci nos seus "pontos de crescimento". Quando a planta tem um novo rebento, leva dois meses a crescer até que as ramificações fiquem sufecientemente fortes. Se a planta ramifica todos os meses, depois disso, no ponto de ramificação, obtemos uma figura semelhante à de baixo:

Desde
o século XIX vem-se descobrindo fatos intrigantes
sobre sequência de Fibonacci.
O
applet abaixo mostra um deles, em que cada termo representa
a medida do lado de um quadrado. Esses
quadrados, quando dispostos convenientemente lado a lado,
vão formando retângulos cujos lados são
termos consecutivos da sequência de Fibonacci. (clique
no botão com a legenda Fibonacci).
Observando-se
a tabela, podemos notar que a razão entre o
comprimento (C) e a largura (L) de cada retângulo, que
é o mesmo que a divisão entre dois termos
consecutivos da sequência, vai tendendo ao número
áureo 1,6180339887...
No limite,
quando n tende ao infinito, a razão f(n)/f(n-1)
é a própria razão áurea
e o retângulo de lados f(n) e f(n-1) é o retângulo
áureo.
Este applet mostra a construção da espiral de
Fibonacci a partir de rectangulos de ouro.
Clicar no botão PLAY para começar a
construção.
| 11 |
101 |
1001 |
10001 |
100001 |
1000001 |
... |
| 1 |
3 |
6 |
10 |
15 |
21 |
... |
| 1 |
6 |
11 |
16 |
21 |
26 |
... |
No
Fundo
Queimando
Como
ímpetos
Venta
a impaciência
Gemendo a aplausos da loucura!
Eu,
Sem
Saber
Conversar,
Caneta
na mão,
Compus um poema d’amor!
 |
Voltar ao Início |
|
Voltar
Lista de Actividades |
 |