MATEMÁTICA
E A DEFICIÊNCIA VISUAL
Aline
Luzia Leichtfeld de Araújo – Graduanda em Matemática (FAFIUV)
Fernanda
Marszaukowski – Graduanda em Matemática (FAFIUV)
Orientadora:
Profª. Ms. Marieli Musial (FAFIUV)
Resumo: A
inclusão está cada vez mais presente em nossa realidade. A deficiência visual é
uma das que acontece com maior frequência nas escolas. Para que o aprendizado
deste aluno aconteça de maneira significativa é preciso que escola, professor,
família e demais alunos estejam unidos no processo de inclusão. Ao professor
cabe manipular e adaptar os recursos didáticos de forma que os alunos com
limitação visual possam participar da aula e entender o que está se passando. A
Matemática, considerada por muitos abstrata, faz parte do currículo básico de qualquer
instituição, logo é conteúdo essencial no ensino destes alunos. Os recursos são
de suma importância na aprendizagem desta disciplina, contando também com os
numerais no sistema braile. Devido à preocupação de como utilizar estes
recursos e como ensinar Matemática a cegos e aos com baixa visão, este trabalho
foi desenvolvido para tentar sanar estas dificuldades enfrentadas pelo
professor em sala de aula.
Palavras-Chave:
Matemática,
Aprendizagem, Deficiência Visual.
1.
INTRODUÇÃO
O processo de inclusão de alunos com
necessidades especiais na escola regular nos traz a dura realidade onde estas
instituições muitas vezes não estão preparadas para recebê-los. Ao se tratar de
deficiência visual, juntamente com a deficiência auditiva, são as que fazem
parte com mais frequência do cotidiano escolar.
A
linguagem, comunicação, as expressões culturais e artísticas constituem-se de
imagens e apelos visuais cada vez mais sofisticados. Os conteúdos escolares
privilegiam a visualização em todas as áreas do conhecimento, através de
figuras, mapas, gráficos, letras e números. Assim, as necessidades decorrentes
de alguma limitação visual não devem ser ignoradas. Para que este objetivo seja
alcançado é preciso que as pessoas envolvidas com a educação estejam atentas
aos acontecimentos dentro da escola e dispostos também a aceitar sugestões e
mudanças para melhorar o aprendizado do alunado com esta limitação.
Alunos com
alguma limitação visual terão dificuldades na aprendizagem se não lhe forem
submetidos recursos didáticos em que possam interpretar os conteúdos
apresentados em sala de aula. Por isso cabe ao professor a tarefa de incluir o
aluno em sua classe, adaptando as atividades para a dificuldade de cada aluno.
2.
A DEFICIÊNCIA VISUAL
Segundo Baumel e
Castro (2003), a deficiência visual é explicada em duas categorias a serem
consideradas no processo educativo: cegueira e baixa visão.
A cegueira é uma “alteração grave ou
total de uma ou mais das funções elementares da visão que afeta de modo
irremediável a capacidade de perceber cor, tamanho, distância, forma, posição”.
(SÁ; CAMPOS; SILVA, 2007, p.15). Pode ocorrer desde o nascimento (congênita) ou
posteriormente (adquirida).
As pessoas com baixa visão são
aquelas que apresentam “desde condições de indicar projeção de luz até o grau
em que a redução da acuidade visual interfere ou limita seu desempenho” [1].
Seu processo educativo se desenvolverá, principalmente, por meios visuais,
ainda que com a utilização de recursos específicos.
2.1 ESTATÍSTICAS
O índice de cegueira total nas populações vai de 0,3% a 1,5%, sendo que o
índice de pessoas com baixa visão se considera de 2 a 7% da população total.
Portanto, para cada pessoa cega existem 4 com visão subnormal.
Segundo a OMS, mais de 180 milhões de pessoas no mundo têm deficiência
visual. Dessas, 45 milhões são cegas e 135 milhões têm baixa visão.
Os resultados do Censo 2000 mostram que, aproximadamente, 24,6 milhões de
pessoas, ou 14,5% da população total, apresentaram algum tipo de deficiência.
Dentre esses, 16,6 milhões de pessoas com algum grau de deficiência visual,
onde quase 150 mil se declararam cegos.
[2]
2.2
BAIXA VISÃO
Em geral,
baixa visão é definida como uma condição na qual a visão da pessoa não pode ser
totalmente corrigida por óculos, interferindo com as atividades diárias, assim
como a leitura e a condução. Baixa visão é mais comum entre os idosos, mas pode
ocorrer em pessoas de qualquer idade.
Para que o
educador possa apresentar materiais gráficos compatíveis com as especificidades
individuais do aluno com visão reduzida, ele precisa de informações sobre a
necessidade desse aluno.
2.2.1 O Desempenho
Visual na Escola
Esses alunos manifestam algumas
dificuldades de percepção em determinadas circunstâncias tais como: objetos
situados em ambientes mal iluminados, ambiente muito claro ou ensolarado,
objetos ou materiais que não proporcionam contraste, objetos e seres em
movimento, visão de profundidade, percepção de formas complexas, representação
de objetos tridimensionais. O trabalho com estes alunos deve se basear no
princípio de utilização plena do potencial de visão e dos sentidos
remanescentes, onde o professor deve despertar seu interesse ao conteúdo,
estabelecer o conceito de permanência do objeto e facilitar a exploração
dirigida e organizada.
Como afirma Sá; Campos e Silva, “a
baixa visão pode ocasionar conflitos emocionais psicológicos e sociais, que
influenciam o desempenho visual, a conduta do aluno, e refletem na
aprendizagem.” (2007, p. 18). Logo conhecer o caso e o diagnóstico de cada aluno
torna-se de suma importância para alcançar o aprendizado do mesmo, sendo este
completo e significativo.
2.3 CEGUEIRA
Os sentidos têm as mesmas
características e potencialidades para todas as pessoas. As informações tátil,
auditiva e olfativa são mais desenvolvidas em pessoas cegas devido ao fato
delas recorrerem a estes sentidos com maior frequência para guardar as
informações. Sem a visão os outros sentidos passam a receber os dados de forma
fragmentada, portanto o desenvolvimento dos demais não é um fenômeno
extraordinário, eles trabalham de forma complementar e não isolada.
Os alunos cegos podem e devem
participar de todas as atividades propostas pelo professor com diferentes
níveis e modalidades de adaptação que envolva a criatividade e cooperação entre
os participantes.
2.4 O SISTEMA BRAILE
Criado por Louis Braille em 1825, na
França, o sistema braile é conhecido universalmente como código ou meio de
leitura e escrita de pessoas cegas. Baseia-se na combinação de 63 pontos que
representam as letras do alfabeto, os números e os símbolos gráficos. A
combinação dos pontos é obtida pela disposição de seis pontos básicos,
organizados espacialmente em duas colunas verticais com três pontos à direita e
três à esquerda de uma cela básica denominada cela braile.

Figura 1: cela
braile.
O sistema braile, desde sua criação
passou por várias adaptações. Na área da matemática, o Brasil participou de
várias convenções internacionais que tinham como objetivo “unificar a
simbologia braile para a matemática e as ciências”. (REILY, 2004, p. 146). Em
1963, foi assinado um acordo com Portugal, onde o Brasil passou a utilizar os
símbolos de abreviaturas deste país. Desde 1940 nosso país adotou a tabela
Taylor, elaborada na Inglaterra, para o campo da matemática. Porém
posteriormente devido ao fato da introdução novos símbolos da Matemática
Moderna, houve uma revisão. No Brasil houve uma revisão para a matemática pelo
Código Matemático Unificado em 1997.
Para que um aluno cego consiga
aprender matemática é essencial que conheça os números no sistema braile. Na
figura 2 temos o sistema decimal e os sinais de operação utilizados na
disciplina.

Figura 2: Sistema
Decimal em braile
2.5 ALUNOS COM
LIMITAÇÃO VISUAL EM SALA DE AULA
A predominância de recursos
didáticos visuais ocasiona uma visão fragmentada da realidade e desvia o foco
de interresse e de motivação dos alunos cegos e com baixa visão. A variedade, a
adequação e a qualidade de tais recursos possibilitam o acesso ao conhecimento,
à comunicação e à aprendizagem significativa.
Recursos tecnológicos, equipamentos
e jogos pedagógicos contribuem para que as situações de aprendizagem sejam
agradáveis e motivadoras para alunos com limitação visual.
Os recursos ópticos
são de suma importância para o aprendizado de alunos com baixa visão. Lentes,
lupas, óculos, telescópios são exemplos de recursos desse tipo utilizados pelos
alunos em sala de aula. Porém o uso destes instrumentos depende do caso de cada
aluno, logo não são todos que utilizam.
Recursos não-ópticos são aqueles que
auxiliam os alunos com baixa visão a serem independentes em sala de aula.
Alguns exemplos destes recursos são: ampliação das fontes, sinais e símbolos em
livros, cadernos; carteira adaptada (inclinada); cadernos com pautas pretas
espaçadas, guia de leitura (tiposcópios), gravadores; chapéus e bonés; CCTV (circuito
fechado de televisão) que amplia até 60 vezes as imagens.
A configuração do espaço físico da
sala de aula não é percebida de imediato pelo aluno cego como acontece com os
que enxergam. A coleta de informações se dará através da exploração do espaço:
entrada da escola, pátio, banheiros e outros. Qualquer alteração feita deve ser
avisada aos alunos, a fim de que estes possam mover-se pela escola, pois sua
memória codifica onde estão os mobiliários.
3.
MATEMÁTICA PARA DEFICIENTES VISUAIS
Na deficiência
visual, materiais e recursos assumem papel e função importantes com base nos
requisitos e quadros apresentados nessa deficiência. Assim em relação aos professores cabe a cada
um
estabelecer
um processo de desenvolvimento profissional, caracterizando sua prática
pedagógica como inovadora e criativa, baseada no uso e na análise dos materiais
e recursos, considerando-os suportes do ensino. Nesta questão, o incentivo à
formação continuada e a busca de aperfeiçoamento pessoal e profissional do
professor são, sem dúvida, condições cruciais para experimentos e análises do
grau de inovações advindas dos materiais. (BAUMEL; CASTRO, 2003, p.106)
O campo da matemática
hoje abrange muitas competências, incluindo geometria, aritmética, álgebra,
estatística, etc. Em matemática não se opera apenas com números, mas também com
relações, classes, conjuntos e agrupamentos, entre outros. Para dar conta desta
variedade de conceitos, os sistemas de representação tornaram-se complexos, atingindo
graus de abstração que desafiam os educadores do ensino fundamental e médio. De
fato, como afirma Reily, “sem recursos especiais alunos com cegueira terão
bastante dificuldade de acompanhar a matéria nas primeiras séries do ensino
fundamental, bem como a partir da 5ª série, quando as exigências começam a
aumentar.” (REILY, 2004, p.60).
Algumas atividades predominantemente
visuais devem ser adaptadas com antecedência e outras durante sua execução por
meio de descrição, informação tátil, auditiva, olfativa e qualquer outra
referência que favoreça a compreensão do ambiente. Os esquemas, símbolos e
diagramas presentes devem ser descritos oralmente. Os desenhos, gráficos e
ilustrações devem ser adaptados e representados em relevo.
Existem algumas soluções já
utilizadas em sala de aula com alunos cegos ou com baixa visão, como o sorobã e
o cubaritmo. Outros recursos utilizados na escola comum para auxiliar o
aprendizado de matemática são os blocos lógicos, o material dourado, o
cuisenaire, o tangran.
Outro instrumento bem conhecido que
pode ser utilizado em sala de aula é o dominó, com os pontinhos que representam
os números em relevo.
Nas séries iniciais do ensino
fundamental pode ser utilizado para fixação e compreensão entre o número e a
quantidade que ele representa usando a caixa de números. Onde na parte externa
é colocado o numeral, em relevo e em braile que corresponde à quantidade de
objetos guardados dentro da caixa (figura 3).

Figura 3: Caixa de
números.
3.1 O MULTIPLANO
O
Multiplano é apresentado como alternativa concreta que facilita a aquisição do
raciocínio matemático, ferramenta essencial a qualquer ser humano. Com ele,
muitas são as possibilidades de uso, desde operações simples às complexas, o
que permite que a matemática seja analisada sob enfoque global e não por
parcelas separadas de conteúdo.
Este material foi planejado pelo
professor Rubens Ferronato desde 2000, diante da série de dificuldades
enfrentadas por ele ao ensinar conteúdos matemáticos a um aluno cego.
Considerando as mínimas condições que as escolas possuem em relação aos métodos
e materiais didático-pedagógicos, impossibilitando assim uma maior interação do
ensino-aprendizagem e no vínculo que este possui com o cotidiano do aluno.
Hoje o multiplano está sendo utilizado por
pessoas com necessidades educacionais especiais, em específico, os deficientes
visuais. Este recurso possibilita ao estudante a compreensão da lógica
existente nos conteúdos matemáticos e configura-se como elemento decisivo para
o entendimento e proposições de alternativas na superação de problemas
vivenciados nesta área.
Conteúdos aplicados: operações,
tabuada, equações, proporção, regra de três, funções, matriz,
determinantes, sistema linear, gráficos de funções, inequações, funções
exponenciais e logarítmicas, trigonometria, geometria plana e espacial,
Estatística, entre outros. Através do toque permite ao estudante, perceber o
sentido das operações matemáticas, pelo fato da percepção ser decorrente também
do tato. O contato com este material pedagógico possibilita o entendimento da
construção de fórmulas matemáticas, porque o estudante passa para a construção
lógica do problema a partir da experimentação concreta. Assim, o aluno
compreende o processo lógico que levou ao resultado e como se processa na prática.
O multiplano é composto pelo multiplano
retangular que possui 546 furos, onde são feitos os cálculos e gráficos; temos
também o multiplano circular que possui 72 furos na circunferência distribuídos
de cinco em cinco graus. Os pinos têm várias aplicações como: fixar o elástico,
indicar a posição, entre outras; além disso, o pino com superfície esférica
indica números positivos e intervalos fechados nos números reais, e o pino com
superfície plana representa os números negativos e intervalos abertos nos
números reais. Os elásticos são usados para representar figuras geométricas,
intervalos, entre outros. As hastes são utilizadas para representar sólidos
geométricos, gráficos das funções. Nas figuras abaixo (4 e 5) temos as
representações de alguns casos no multiplano.

Figura 4: Gráficos no multiplano: parábola (função
do segundo grau), reta (função do primeiro grau) e de barras (usados na
Estatística).

Figura 5:
quadrado; fração (utilizando pinos e elásticos); subtração (pinos com marcação
braile e indú-arabico).
3.2 CUBARITMO
O cubaritmo é composto de uma grade
onde se encaixam cubos com pontos em relevo do sistema braile de escrita
numérica em cada um dos seis lados (os quatro pontos superiores),
correspondendo aos numerais de 0 a 9 (figura 6), além de uma face lisa e uma
face com um traço (que será utilizado como separador na operação).










Figura 6:
Representação dos números em braile no cubaritmo
Como vemos na figura acima, basta
virar os cubos e teremos que o 2 pode representar o 2 e o 3; 1 é único; 4 pode
representar o 4, 6, 8 e 0; 5 pode representar o 5 e 9; 7 é único.
Calcula-se
mentalmente o resultado, da direita para a esquerda, escrevendo-se o resultado
na linha seguinte, sem tirar nem pôr, como quem enxerga faria à tinta no papel.
O
cubaritmo permite que o aluno relacione a matemática com os caracteres em
braile. Este material permite o ensino básico desta ciência nos primeiros anos
do ensino fundamental.

Figura 7: Cubaritmo.
3.3 SOROBÃ
O sorobã (figura 8), conhecido também
como ábaco, tem origem ocidental com a finalidade de contar e realizar
operações matemáticas. No Brasil foi adaptado para ser utilizado por pessoas
cegas.
Trata-se
de uma moldura separada por uma régua em duas partes horizontais, a inferior e
a superior. A régua é dividida em seis partes iguais, com pontos salientes de
três em três hastes, representando as unidades, dezenas e centenas de cada
classe. Há 21 hastes verticais, em que se movimentam as contas, sendo que, na
parte inferior, cada haste tem quatro contas e, na superior, uma. (REILY, 2004,
p. 62).
Para registrar as operações, o aluno
coloca o instrumento na posição zerada, isto é, com todas as contas afastadas
da régua central, encostadas nas paredes do sorobã. E utilizando os dedos
indicador e polegar vai movendo as contas conforme o desejado.
O instrumento permite a realização
das quatro operações: adição, subtração, multiplicação e divisão; onde se
registra os numerais, sendo que o cálculo é feito mentalmente. Embora adaptado
para pessoas cegas e com baixa visão, o sorobã pode ser utilizado por qualquer
aluno.

Figura 8: Sorobã.
4.
CONSIDERAÇÕES FINAIS
Todas as crianças têm
direito à educação pela atual LDB (Leis de Diretrizes e Bases da Educação) e às
que possuem necessidades especiais, amparadas pela mesma lei têm direito a
frequentar a escola regular. Para que este aluno seja incluso verdadeiramente
em sala de aula é preciso que todos os membros da escola estejam unidos para a
realização de tal missão.
Quando se trata de um aluno com
deficiência visual, vários cuidados precisam ser tomados, sendo um deles o
espaço físico da escola, que precisa ser adequado e quando houver mudança,
comunicado aos alunos. As crianças com necessidades especiais têm os mesmos
direitos que aquelas que não as possuem. No entanto, deve-se levar em
consideração que estas crianças precisam de cuidados especiais. Em relação ao
ensino, o professor deve propor atividades onde todos os alunos trabalhem
juntos. Para que a aprendizagem ocorra de maneira significativa é necessário
que se usem os recursos didáticos e o professor os adapte para a situação em
que se encontra o aluno com limitação visual.
Assim como nas outras disciplinas, a
Matemática também precisa ser adaptada para os alunos com deficiência visual,
tendo várias alternativas, recursos e maneiras de torná-la interessante aos
olhos do aluno. Jogos, brinquedos e materiais adaptados ajudam para que os
conteúdos matemáticos tornem-se mais divertidos, fazendo com que estes alunos
aprendam esta disciplina.
5.
REFERÊNCIAS
BAIXA VISÃO.
Disponível em: <http://www.vejam.com.br/baixavisao-quem-tem/>. Acesso em:
11 out. 2009.
BAUMEL, R. C. R. C;
CASTRO, A. M de. Materiais e Recursos de Ensino para Deficientes Visuais. In:
RIBEIRO, M. L; BAUMEL, R. C. Educação
Especial: Do querer ao Fazer. São Paulo: Avercamp, 2003, p. 95 – 107.
DEFICIÊNCIA
VISUAL. Disponível em:
<http://www.laramara.org.br/portugues/conteudo.php?id_nivel1=1&id_nivel2=52&nome=LARAMARA>.
Acesso em: 28 set. 2009.
REILY, L. Escola Inclusiva: Linguagem e mediação.
Campinas: Papirus, 2004. (Série Educação Especial).
SÁ, E.D. de; CAMPOS,
I.M. de; SILVA, M. B. C. Atendimento
Educacional Especializado: Deficiência Visual. São Paulo: MEC/SEESP, 2007.
BIBLIOGRAFIA
CONSULTADA
MULTIPLANO.
Disponível em: <http://www.multiplano.com.br/>. Acesso em: 21 set. 2009.
MULTIPLANO:
UM AVANÇO NA MATEMÁTICA. Disponível em: <http://www.multiplano.com.br/>.
Acesso em: 21 set. 2009.
RECURSOS
DIDÁTICOS NA EDUCAÇÃO ESPECIAL. Disponível em:
<http://www.ibc.gov.br/Nucleus/index.php?itemid=102#more>. Acesso em: 11
out. 2009.
SISTEMAS NUMÉRICOS
Das bases antigas até as atuais
Diogo da Silva Gomes de Pinho – Graduando em
Matemática (FAFIUV)
Orientador: Prof. Celso Silva (FAFIUV)
RESUMO
Os sumérios, um dos
povos habitantes da mesopotâmia, considerada a civilização mais antiga da
humanidade, foram os inventores da escrita cuneiforme, por volta de 5.000 anos
atrás. A evolução dessa cultura fez surgir a necessidade de registros fixos dos
seus atos e idéias para auxiliar o trabalho prático. Com a evolução da referida
cultura surgiu a necessidade de uma escrita própria e também uma representação
de quantidades que os facilitaria no dia-a-dia. O estudo desse progresso, que
foi em grande parte babilônico, revela a criação do sistema numérico
sexagesimal. Este junto ao já existente sistema de base dez, durante muito
tempo serviu como base para representar uniformemente quantidades específicas
de objetos com as mesmas características. Com base em pesquisas bibliográficas
em torno de grandes trabalhos do objeto, em várias épocas da história,
percebe-se que essa representação se preserva até hoje e fundamenta algumas
peculiaridades do nosso cotidiano. Assim como a base sexagesimal, outras bases,
também criadas com a intenção de reunir objetos para facilitar a contagem,
terão sua criação evidenciada. Embora muita gente desconheça a origem dos
números e das suas representações, torna-se necessário um estudo mais profundo
da procedência destes para um melhor entendimento e até aproveitamento dos
recursos que os mesmos nos disponibilizam como o calendário gregoriano e a
contagem de horas e derivados, pesos e sistemas métricos.
Palavras-chave: sistemas numéricos,
criação, evolução.
1 INTRODUÇÃO
Questões filosóficas de onde viemos, por que
viemos, entre outras, são feitas em relação a nossa vida e tudo que faz parte
dela. Tudo há um começo e um porque, este artigo visa focar diretamente em
relação a origem dos números.
Foram
várias as formas de contar ao longo da história do homem, diversos sistemas de
numeração foram criados por diferentes civilizações. Observando apenas
este lado matemático, é possível perceber a diversidade cultural existente
dentro de um mesmo ambiente, pois em alguns casos mais de um sistema numérico
foi criado, com a mesma intenção, porém com maneiras de trabalhar diferentes.
Todos
estes sistemas foram criados para facilitar a contagem. Mas mesmo com todo o
avanço de cada um deles ainda era difícil calcular. Em alguns, eram muitos
símbolos para representar um número e escrever um valor grande era difícil. Com
o passar dos tempos os sistemas foram se aprimorando e então o sistema
hindu-arábico foi difundido, este que é o usado atualmente.
Será
esclarecida também a maneira que eles eram trabalhados e como eles foram úteis
e oportunos pra vida daqueles que os criaram. Existiram vários sistemas
numéricos que não serão citados neste trabalho. Aqui ater-me-ei a dissertar a
respeito dos sistemas mais conhecidos e amplamente usados pelos povos antigos.
É importante frisar que estas civilizações não vieram umas depois das outras.
Pelo contrário, muitas coexistiram durante séculos e, embora localizadas em
regiões diferentes, mantiveram contato umas com as outras.
2 ANTES DOS NÚMEROS – CONTEXTO HISTÓRICO.
Durante
muito tempo, os homens viviam de forma a contentar-se com o seu bem-estar
momentâneo. Faziam de tudo para que o seu “agora” fosse o melhor possível, para
isso ele e sua comunidade desenvolviam hábitos que lhe facilitavam o convívio e
a melhora na qualidade de vida. Entre vários aspectos, os seres da pré-história
tinham uma característica muito marcante, durante um longo período foram
nômades.
O
nomadismo, de acordo com Ximenes (2001) consiste em uma prática onde um homem
ou grupos humanos vagueiam por diferentes territórios, nesse processo de
locomoção pelo espaço, essas comunidades utilizam-se dos recursos oferecidos
pela natureza até esses se esgotarem, com o fim desses benefícios, tais grupos
se deslocam até encontrarem outra região que ofereça as condições necessárias
para a sobrevivência.
Porém com
o passar do tempo, houveram mudanças climáticas e o homem acidentalmente
descobriu a vantagem de plantar. Alguns indivíduos notaram que alguns grãos que
eram coletados da natureza para a sua alimentação poderiam ser enterrados a fim
de produzir novas plantas iguais às que os originaram. Essa prática permitiu o
aumento da oferta de alimento dessas pessoas que perceberam que se as plantas
fossem cultivadas próximas uma das outras elas poderiam produzir frutos, que
seriam facilmente colhidos quando chegassem ao ponto certo.
Rebola
(2004) compreende e mostra que as freqüentes buscas à procura de alimentos eram
desnecessárias, já que eles perceberam que era só plantar que depois de um
tempo, eles teriam mais. Então de posse de um determinado local, a comunidade
começou a se desenvolver, administravam a reprodução dos animais e o cultivo de
plantas. Então, aos poucos, o homem deixou de ser nômade e passou a ser
sedentário. Houve uma mudança extrema na vida do ser humano, se antes ele saía
em busca do alimento, agora ele aprendeu a produzir o seu próprio, construiu
casas, proteções e fortificações para evitar que outros grupos que não tinham o
mesmo pensamento desenvolvimentista lhe tomassem o que foi produzido.
Aos poucos
ele foi percebendo que determinada época do ano era propícia a determinada
atividade e imprópria a outras, percebeu também que o tempo, as estações do ano
e as fases da lua, também influenciavam bastante. Com isso foram criadas formas
primitivas do que hoje é o nosso calendário.
Ao longo
de todos esses anos o homem usava de varias formas pra “contabilizar” as coisas
que queria, embora não tivesse noção específica do que era o princípio da
contagem. Durante muito tempo eles usavam objetos e partes do corpo como
parâmetros de quantidade. Esses instrumentos foram se aperfeiçoando até chegar
ao que usamos hoje, os números indo-arábicos.
Um fato
bem conhecido e que mostra parcial e vagamente o inicio do entendimento no
processo de contabilidade é o desenvolvimento do sistema um por um, Ximenes
(2001). Os pastores tinham um trabalho muito simples, de manhã bem cedo, eles
levavam as ovelhas para pastar. À noite as recolhiam, guardando-as dentro de um
cercado. Para ter o controle da quantidade, ver se não estava esquecendo
nenhuma, ou se alguma ovelha havia sido devorada por um animal selvagem ele
resolveu contar as ovelhas com pedras.
Assim, cada ovelha que saía para pastar correspondia a uma pedra. O pastor
colocava todas as pedras em um saquinho. No fim do dia, à medida que as ovelhas
entravam no cercado, ele ia retirando as pedras. Se sobrassem pedras, então ele
provavelmente perdeu animais, caso faltassem pedras, ele ganhou algum animal
vindo perdido de outro rebanho, ou ele perdeu alguma pedra.
O que eles
tinham até então era o senso numérico e não a capacidade de contar propriamente
dita, que é um atributo exclusivamente humano que necessita de um processo
mental. Uma ilustração disso é o caso do corvo.
Rebola
(2004) afirma que até então o que acontecia com os homens pré-históricos era o
mesmo que acontece com os animais irracionais, eles têm noção da quantidade de
uma forma ampla, mas são incapazes de realizar operações com elas, nem mesmo
trabalhar de alguma outra forma com esses dados.
Foi
contando objetos com outros objetos que a humanidade começou a construir o conceito de número.
Para o homem primitivo o número cinco, por exemplo, sempre estaria ligado a alguma coisa
concreta: cinco dedos, cinco peixes, cinco bastões, cinco animais, e assim por
diante. A idéia de contagem estava relacionada com os dedos da mão. Os
caçadores contavam os animais abatidos, traçando riscos na madeira ou fazendo
nós em uma corda, também de cinco em cinco. E é pela sua facilidade na
associação com outras coisas que este foi o primeiro sistema de base numérica,
o cinco é então um número concreto que durante muito tempo foi considerado o
numero-chave. Por não ser até então um conceito amplo, cada região criou um
sistema de numeração que fosse apropriado a seu povo, e que seria facilmente
entendido por todos.
3 ANTIGOS SISTEMAS NUMÉRICOS
3.1 SISTEMA NUMÉRICO EGÍPCIO
A
civilização egípcia surgiu a partir do agrupamento de várias tribos africanas e
asiáticas à beira do rio Nilo, no nordeste da África, cerca de cinco mil anos
atrás. O rio Nilo era muito importante para a vida deste povo, desta fonte eles
usavam a água para beber, cultivo de plantas e peixes para alimentação.
Como
afirma Ifrah (1998) A atividade agrícola era muito bem organizada o que
propiciou para que os agricultores passassem a produzir alimentos em
quantidades superiores às suas necessidades. Com isso algumas pessoas puderam
se dedicar a outras atividades, tornando-se artesãos, comerciantes,
sacerdotes. Diante de tanto desenvolvimento algumas tarefas foram ficando
cada vez mais difíceis de serem realizadas sem algo que sustentasse suas idéias
e ações práticas. Como por exemplo, anotar a quantidade de territórios que
deveriam ser cultivados, a época certa em que haveria a cheia e o espaço que
seria ocupado pela elevação das águas, a quantidade de material, ou mesmo de
pessoas para trabalharem na construção das pirâmides.
Os
egípcios marcavam, desenhavam, listavam e calculavam. Porém de uma forma que só
eles entendiam, através de hieróglifos (escrita com figuras) e com os números
por eles desenvolvidos.
Para Ifrah
(1998), para o sistema foram criados desenhos que representariam determinada
quantidade. Há varias hipóteses para a explicação do
significado de cada desenho, uma delas é que o símbolo do número um é
um pedaço de corda estirado. Juntando vários desses pedaços nós ficamos
com um pedaço maior, que se curva. Este pedaço de corda curvado era o símbolo
para dez. Juntando mais pedaços de corda nós teríamos uma corda ainda maior,
que poderia ser enrolada. O desenho de um rolinho de corda era o que representa
cem unidades. Para representar o mil era utilizada a flor de lótus, símbolo da
beleza. Para dez mil, os egípcios desenhavam o dedo do faraó,
que representava poder; para cem mil, desenhavam um girino ou um sapo, que
naquela cultura simbolizava fertilidade. E, finalmente, a representação de
um milhão era feita com a figura de um sacerdote louvando os deuses. E com
apenas estes símbolos, era possível escrever qualquer outro número.

Figura
1: Sistema de numeração egípcio
Fonte: http://www.invivo.fiocruz.br
Imenes
(1999) sobre esse assunto dizia que quando escreviam seus números, os egípcios
não se preocupavam com a ordem dos símbolos. Para ler era só somar tudo. É por
isso que nós chamamos este sistema numérico de não-posicional e aditivo. Era
também um sistema decimal, pois trabalhavam sempre com grupos de dez. Assim, o
numero 315, por exemplo, poderia ser escrito de outra forma, que combinasse a
mesma quantidade dos determinados símbolos.
![]()
Figura
2: Exemplo do número 315
Fonte: http://www.invivo.fiocruz.br
3.2
SISTEMA NUMÉRICO MESOPOTÂMICO (BABILÔNICO E SUMÉRIO)
A
Mesopotâmia ocupou territórios onde atualmente se situam o Iraque, parte do
Irão e parte da Síria até ao Golfo Pérsico. Foi aí que as primeiras sociedades
urbanas surgiram e onde, um pouco antes do fim do IV milênio a.C., apareceu a
primeira escrita. Povos de diferentes etnias ocuparam a Mesopotâmia,
destacando-se os Sumérios, os Acádios e, posteriormente, os Amoritas, Hititas,
Hurritas, Assírios, Elamitas, Cassitas, Medos e Persas.
Conway,
(1999) diz que os Sumérios possuíam uma civilização avançada com uma
organização social e econômica complexas, estruturas políticas e religiosas.
Como os recursos naturais eram escassos, as trocas comerciais com os povos
vizinhos revestiam-se de grande importância. Desta forma, e com o aumento do
volume de trocas comerciais, torna-se necessário um controle administrativo
mais eficaz. Os sistemas de registro foram-se desenvolvendo num complexo
sistema numérico que permitia registrar grandes quantidades de bens.
Da
civilização mesopotâmica recebemos um considerável número dos nossos elementos
culturais mais comuns: o ano de doze meses e a semana de sete dias; o fato de
os mostradores dos nossos relógios conterem os números de um até doze,
correspondentes à divisão caldaica do dia em doze horas duplas; a crença nos
horóscopos; a superstição de fazer o plantio de acordo com as fases da lua; os
doze signos do Zodíaco; o círculo de 360 graus.
Segundo
Guelli (2004) o sistema numérico mesopotâmico assemelha-se do egípcio, porem a
matemática mesopotâmica atingiu um nível mais elevado. Neste sistema aditivo,
onde cada figura representa um valor e para se descobrir o número escrito basta
você somar as quantidades respectivas das figuras, porém difere-se no seu
sistema de colocação, já que este é posicional, ou seja, a ordem em que o
número é escrito influencia diretamente no seu resultado final. Enquanto os
egípcios indicavam cada unidade mais elevada através de um novo símbolo, os
mesopotâmicos usavam o mesmo símbolo, mas indicavam o seu valor pela sua
posição.

Figura 3:
Sistema de numeração mesopotâmico (Babilônico / Sumério)
Fonte:
http://www.mundoeducacao.com.br
Como eles
só haviam inventado números ate o cinqüenta e nove, a partir daí eles teriam
que escrever os próximos números em forma de combinação dos já existentes. De
maneira que eles representavam a quantidade de vezes que a base aparecia. O
numero 60 é representado da mesma maneira que o número 1, porém tem uma outra
interpretação e deve ser visto como uma vez a base 60 (1 x 60 = 60), já o
número 82, é feito de forma que fique
clara a soma 60 + 20 + 2 [ 1x(601) + 2x10 + 1x2]. E a representação
de números maiores vai complicando cada vez mais. Apesar de usarem as mesmas
figuras pro mesmo número, eles entendiam qual era o número de acordo com o
contexto, ou seja, eles não confundiam o 1 com o 60 por exemplo. O 11. 040 era
representado de forma que [ 3x(60²) + 4x(60)], e o 524.551 como [2x(60³) +
25(60²) + 42(60) + 3(10) + 1].
A
numeração mesopotâmica exigia assim repetições, singularmente extensas, de
sinais idênticos, já que se apoiava no princípio da justaposição dos símbolos
pela simples adição de valores. Ifrah (1997) apresentou como exemplo desta
situação o caso do número 3599 para cuja representação seriam necessários 276
pictogramas.
![]()
Figura
4: Exemplos de números escritos no sistema mesopotâmico
Fonte:
http://www.mundoeducação.com.br
Segundo
Mateus (2004) esse sistema de numeração durou até um tempo, mas depois acabou
sendo posto em dúvida, justamente pela falta de um símbolo quer representasse o
zero, o que algumas vezes causava alguns mal-entendidos.
3.3 SISTEMA NUMÉRICO
GREGO.
A
história da civilização grega tem suas origens nas invasões de povos bárbaros
(dórios, aqueus, jônicos e eólios), na península balcânica por volta do ano
2.000 a.C. Estes povos foram conquistando as civilizações ali estabelecidas e
avançando em direção à ilha de Creta.
Silva
(2000) dizia que os filósofos de Mileto, entre eles Tales, começaram a tentar
compreender os fenômenos da natureza sem recorrer a mitos e à religião. A
utilização do raciocínio dedutivo deu origem à criação de uma matemática
dedutiva e formalmente organizada, bem diferente da matemática de caráter
iminentemente prático, desenvolvida no Egito e na Mesopotâmia.
Os
gregos são considerados pais da democracia e da filosofia. Crê-se também
que eles foram os responsáveis pelo desenvolvimento de algumas ciências, como a
medicina. Hoje em dia grande parte do desenvolvimento da matemática se deve aos
gregos, nomes como Pitágoras, Tales de Mileto, Platão, Euclides, Diofanto,
Papus.
Por
volta de 800 a.c. os gregos mudaram do sistema de escrita hieroglífica para o
alfabeto fenício. Isto os permitiu transmitir por escrito a sua literatura,
utilizando o papiro. Eles fizeram algumas modificações no sistema de
numeração que utilizavam, no qual os números eram representados pelas letras
iniciais de seus nomes. A partir das mudanças, surgiu um novo sistema numérico,
onde todas as letras do alfabeto gregos mais três letras do alfabeto fenício
eram utilizadas como símbolos numerais.

Figura
5: Sistema de numeração grego
Fonte: http:// www.invivo.fiocruz.br
![]()
Figura 6: Exemplo de
números escritos através do sistema grego.
Fonte: http:// www.invivo.fiocruz.br
Para
representar milhares até 10.000 fazia-se uma marca à esquerda da letra. Por
exemplo:
6751 em
numeração grega escreve-se ‘V y n a ;
Para
números superiores ou iguais a 10.000 usava-se a letra M para representar dez
milhares.
23.000 em
numeração grega escreve-se Mb 'g (2x
10.000+3000);
71.750.000
em numeração grega escreve-se M¢ z r o e
((7x1000+100+70+5)x10.000).
Tem sido
argumentado que este sistema alfabético foi prejudicial ao desenvolvimento da
álgebra grega, porque o uso de letras para representar os números em geral, tal
como fazemos na nossa álgebra atual, pode tornar-se complicado.
3.4
SISTEMA NUMÉRICO ROMANO
De acordo
com os historiadores, a fundação de Roma resulta da mistura de três povos que
foram habitar a região da Península Itálica: gregos, etruscos e italiotas. Desenvolveram na região uma economia
baseada na agricultura e nas atividades pastoris. O sistema político era a
monarquia, já que a cidade era governada por um rei. Os
etruscos eram chamados de “tirrenos” pelos gregos e dominaram a região por
muito tempo, transformando a pequena aldeia de pastores em uma cidade. Começava
assim a história do grande império, que organizou um forte exército, dominou
dezenas de outros territórios, como a Grécia, o Egito, a Macedônia, a Gália, a
Germânia, a Trácia, a Síria e a Palestina. Há cerca de 2.200 anos, já era o centro econômico e
político da região que cercava o Mar Mediterrâneo. Com as conquistas, a
vida e a estrutura de Roma passaram por significativas mudanças. O império
romano passou a ser muito mais comercial do que agrário. Povos conquistados
foram escravizados ou passaram a pagar impostos para o império.
Estas
são apenas algumas informações sobre a civilização romana, era um povo tão
importante e com tantas terras, autoridades, prédios que não poderia deixar de
lado os números.
O
latim, língua dos romanos, foi adotado por muitas regiões de seu império e foi
muito além, pois deu origem às outras línguas, como o português, espanhol,
francês e o italiano. Por isso os números romanos foram difundidos e adotados
por muitos povos, estando presentes ainda hoje.
Sabe-se
muito pouco a respeito da origem da notação romana para números. Os romanos
nunca usaram as letras sucessivas de seu alfabeto para propósitos de numeração,
como faziam algumas civilizações antigas. Até Roma tornar-se o grande império
que foi, os etruscos usavam numerais que se assemelhavam às letras de seu
próprio alfabeto e também os numerais usados pelos romanos. Até chegar a forma
que conhecemos hoje, esse sistema numérico passou por varias reformas, desde a
forma em que é escrito, até na seqüência de um símbolo.

Figura 7:
Algumas transformações dos números romanos.
Fonte: http://www.educ.fc.ul.pt
Como
exemplo de mudança na sua estrutura temos que, inicialmente eles usavam somente
o princípio aditivo, fazendo com que um símbolo pudesse ser repetido até quatro
vezes, porém com a reforma, foi incluso o princípio subtrativo, tornando
possível a repetição apenas três vezes de um mesmo algarismo e na hora de
escrever mudaria a ordem do símbolos. A tabela a seguir mostra de que forma
eram os símbolos.
|
Letras |
Valores |
|
I |
1 |
|
V |
5 |
|
X |
10 |
|
L |
50 |
|
C |
100 |
|
D |
500 |
|
M |
1000 |
Tabela 1:
Representação final dos numerais romanos
Fonte: Menninger (1958)
Menninger
(1958) concluiu que para escrever um número basta fazer a combinação destes da
tabela, atendo-se a regra de sempre usar no máximo três vezes um mesmo número, quando um
sinal está à esquerda de outro com valor superior, diminui-se dele, quando está
à direita, soma-se.
Exemplo:
Para escrever o número três repete-se três vezes o símbolo I, 3 = III. O 6 é VI
(5+1). Inicialmente para escrever o número quatro, repetia-se o I quatro vezes,
porém ficou decidido que a partir do princípio subtrativo o quatro seria IV (5
– 1).
Para
representar um número na casa do milhar, a partir do quatro mil, eles usavam
colocar um traço horizontal sobre este, e dos milhões, duas barras.

Figura 8:
Números em milhares no sistema romano.
Fonte:
Guelli
3.5 SISTEMA NUMÉRICO CHINÊS – JAPONÊS.
A
civilização chinesa desenvolveu-se ao longo das margens do rio Amarelo e do
Azul, desde o 3º milênio a.C. durante a dinastia Hsia iniciada pelo
imperador Yu, que era
tido como grande conhecedor das águas subterrâneas, cujos veios descobria
facilmente. Confúcio, um dos maiores pensadores chineses e a figura mais
conhecida na história da China como mestre, filósofo e teórico político, disse
que o imperador "dominou as grandes inundações". Os chineses primavam
por sua habilidade em investigações ao subsolo, e proibiam a localização de
casas e abrigos de animais em cima das chamadas "Veias do Dragão", ou
"Saída dos Demônios", arte conhecida como FENG SHUI. Desta dinastia
provêm os primeiros numerais chineses inscritos sobre carapaças de tartarugas e
ossos de animais.
O grande
império desintegra-se, por volta do 700 a.C.. Aproximadamente até 400 a.C., a
China é um conjunto de estados independentes em permanente guerra uns com os
outros. É desta altura o primeiro texto sobre matemática - o Chou Pei Suan Ching, que além de
falar sobre cálculo aritmético falava sobre as propriedades dos triângulos
retângulos de acordo com o teorema de Pitágoras.
De acordo
com Colonese, entre os sistemas de numeração
mais antigos encontra-se o utilizado pelos chineses e mais tarde adotado também
pelos japoneses. Este sistema passou por várias transformações, e todas visavam
à melhoria e a desambiguação dos números para melhor representação dos mesmos,
era baseado em recursos gráficos com muitas formas abstratas e combinações de
sinais arcaicos.
Um traço
horizontal simbolizava a unidade, dois traços duas unidades e, analogamente,
para três e quatro. A incapacidade de identificar diretamente uma série de mais
de quatro sinais idênticos não permite que este processo se repita
continuamente. Sendo assim, para representar o algarismo 5, utilizavam traços
que formavam um X fechado em cima e em baixo. O algarismo 6 era simbolizado por
um V invertido ou ainda por um desenho em forma de templo. Para o algarismo 7
era utilizada uma cruz e duas semi-circunferências de "costas" uma
para a outra eram o símbolo utilizado para o algarismo 8. Para o 9 era usado um
símbolo que faz lembrar o anzol.
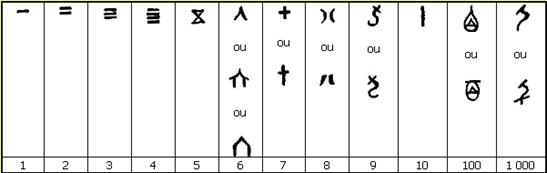
Figura 9: Primeiro sistema numérico Chinês
Fonte:
http://www.educ.fc.ul.pt
O
chinês foi o primeiro sistema numérico que utilizou do princípio multiplicativo
direto juntamente com o aditivo. Para números maiores que dez, exceto o cem e o
mil eles usavam a combinação dos símbolos para formar os outros. Por exemplo, o
número onze, era formado pela junção do símbolo do dez, com o do um, o doze, o
dez e o dois, e assim por diante, porém o símbolo da dezena era sempre
acrescentado na parte inferior dos números.

Figura 10: Sistema numérico Chinês
Fonte:
http://www.educ.fc.ul.pt
Diferente
do sistema mesopotâmico, que também usava um princípio multiplicativo, o chinês
formava o número usando o somatório do produto dos números, ao contrario do
primeiro que só representava a multiplicação para indicar a base sessenta.
Há várias
hipóteses que explicam os símbolos escolhidos pra representar os números,
pensa-se que podem ter sido criados à semelhança fonética que existia entre o
símbolo e a palavra oral correspondente aos algarismos. Mas esta não é a única
explicação, a escolha pode também ter sido de ordem religiosa. Como nunca foi
provado nada sobre a origem em si, então não há provas suficientes que
sustentem uma hipótese.
Ao
chegar no vinte, ele une dois símbolos de dez em forma de um “u” maiúsculo. O
trinta é o vinte acrescido de dez, e o quarenta, o vinte mais duas vezes o dez.
Nas dezenas seguintes ele acrescenta o símbolo do dez acima dos números em
unidade. Nas centenas, o princípio de formação era o mesmo dos números de onze
a dezenove, era acrescentado o símbolo de cem abaixo dos números a serem
multiplicados.

Figura
11: Sistema Numérico Chinês
Fonte: http://www.educ.fc.ul.pt
Assim,
para reconhecer um número, bastasse que você identificasse alguns elementos
dele e fizesse a soma dos valores encontrados, diretamente ou como resultado de
uma multiplicação. No exemplo a seguir, temos o numero 1574 que é formado pela
soma das multiplicações 1.000 x 1; 5 x 100; 7 x 10; 4 x 1.

Figura
12: Exemplo de números escritos na base chinesa
Fonte: http://www.educ.fc.ul.pt
Mais
tarde, este sistema sofreu algumas mudanças, estas foram basicamente na forma
de representar os números. Porém, boa parte foi conservada, como por exemplo, a
base dez, a maneira de representar os números que não tinham símbolos
específicos. Eles continuavam utilizando o princípio multiplicativo e o
aditivo. E para formar outros números bastava combinar os específicos.

Figura
13: Sistema numérico mais usado na china
Fonte:
Ifrah
O sistema
numérico chinês foi o que mais teve alterações, até hoje é difícil dizer com
precisão qual foi mais usado, e qual foi o primeiro. Por muito tempo os
sistemas foram usados simultaneamente, o que além de dificultar a confirmação
de hipóteses, torna complicado o estudo temporal das mudanças. Uma das
hipóteses diz que o primeiro apresentado foi o que abrangeu maior território,
porém o segundo teria sido usado por um período maior e com melhor aceitação,
sendo este também utilizado pelos japoneses.
3.6
SISTEMA DE NUMERAÇÃO INDO-ARÁBICO
O
subcontinente indiano foi berço de uma das mais antigas civilizações do mundo,
cobrindo uma área maior que a do Egito e da Suméria. As invasões bárbaras,
nos séculos V e VI d.C. acabaram por destruir o Império Romano e mergulharam o
mundo ocidental num período pouco favorável ao desenvolvimento da Ciência. Mas
enquanto o Império Romano declinava uma grande civilização cada vez aumentava
mais no Oriente, no vale do rio Indo.
Como não
poderia deixar de ser numa sociedade os habitantes da região possuíam uma
linguagem escrita e um sistema numérico. Os hindus tiveram contato com muitas
outras civilizações. Influenciaram-nas e foram influenciadas por elas. O
princípio posicional, presente na numeração hindu, também aparece no sistema
numérico dos babilônios. A base dez, que é uma das características deste
sistema, também era usada pelos egípcios e chineses.
De acordo
com Imenes (2004), um povo que também teve muito contato com os hindus foram os
árabes, estes tiveram um contato muito intenso já que realizavam várias
transações comerciais, o que favoreceu amplamente pra que o sistema hindu fosse
abrangido pelos árabes também, e mais tarde estes foram os que levaram ao
conhecimento de todos o sistema numérico. Um grande mérito deve ser creditado
aos hindus: o de reunir estas diferentes características num mesmo sistema
numérico.
Ifrah
(2007) disserta que assim como todas as civilizações apresentadas até aqui, os
indianos e os árabes também tinham seus sistemas de numeração, com suas
peculiaridades e propriedades. O sistema numérico
indiano, também chamado de hindu, no início, ele era formado por nove símbolos,
que representavam de um a nove. Depois, há cerca de 2.600 anos atrás, eles
criaram um décimo símbolo, para representar o vazio. O zero é uma
característica importante da numeração dos hindus, apesar da criação ser
atribuído a eles há indícios de que, na fase final da civilização babilônia, já
era usado um símbolo para o “nada”, além disso, civilizações como os maias já
usavam um símbolo que representa ausência de uma potência, e a diferença entre
o zero maia e o zero indo-arábico é que este pode tomar qualquer casa decimal
como nula, e no maia, só era usada no meio os algarismos, e nunca como zero no
final, representando a unidade.
Entretanto,
este não era ainda o sistema de numeração que usamos hoje. Muitos séculos se
passaram até que os hindus desenvolvessem o sistema de numeração decimal. Não
há muitos documentos sobre a matemática conhecida pelos hindus da Antigüidade.
Por isto é impossível saber, com exatidão, quando e como os hindus chegaram ao
sistema de numeração decimal posicional. Ao que parece é que, por volta do
século V, eles já o utilizavam.
Para criar qualquer outro número acima do dez,
basta fazer a combinação dos outros números. Usando as casas decimais como
parâmetro pra dimensão do número. Do 0 ate o 9 usa-se apenas a unidade, a
partir do 10 têm-se então uma dezena e zero unidades. E isso por diante, alem
dessas casas decimais temos a centena, milhar e etc.
O sistema
numérico criado pelos romanos foi usado na Europa durante muitos séculos. Isto
aconteceu, sobretudo, devido ao grande poder da Igreja Católica Apostólica
Romana durante toda a Idade Média. O sistema de numeração decimal chegou à
Europa, levado pelos árabes, o que gerou um choque cultural muito grande, já
que os europeus estavam acostumados a lidarem com um tipo de número e depois se
depararem com outro.
Conway
(1999) já dizia que para nós, que conhecemos os dois sistemas, é muito fácil
perceber as enormes vantagens que o sistema numérico decimal tem sobre a numeração
romana. Porém eles naquela época não conseguiram perceber tal diferença. Foram
necessários alguns séculos para que as novas idéias triunfassem
definitivamente. Isto só aconteceu no século XVI.
Durante
muitos anos, uma verdadeira batalha foi travada entre os adeptos do novo
sistema e os defensores do sistema antigo. Os numerais indo-arábicos chegaram a
ser proibidos nos documentos oficiais, mas eram usados na clandestinidade. Essa
aversão não foi suficiente, pois os números indo-arábicos se difundiram e hoje,
são os mais usados e em todos os lugares.

Figura
14: Evolução dos números indo-arábicos
Fonte:
Imenes (2002)
4 CONSIDERAÇÕES FINAIS
Ao estudar
os sistemas numéricos foi possível perceber que toda essa mudança causou muita
polêmica e discussões. Choques de culturas foram inevitáveis já que todos esses
povos tinham contato com outros que não usavam o mesmo sistema, porém isso não
impediu que elas evoluíssem e tivessem suas funções prosseguidas.
Em todos
os casos, os números foram usados amplamente para vários objetivos, como
contagem, resolução de problemas, registro físico de algo e é evidente que se
não fossem criados os sistemas hoje em dia teríamos muitas dificuldades em
tudo. E não é difícil de imaginar, que sem a matemática em si, toda essa
evolução do mundo atual seria inexistente.
Cabe aos
professores ao ensinar os números para os seus alunos, dar um destaque à
criação. Talvez se for dado um enfoque maior a este assunto, os educandos
tenham interesse sobre o tema e desenvolvam maior habilidade.
REFERÊNCIAS BIBLIOGRÁFICAS
SILVA, A. M. Disponível em: http://arkheia.incubadora.fapesp.br. Acesso em: 10 Setembro.
2009.
COLONESE, P. Henrique. Disponível em: http://www.invivo.fiocruz.br.
Acesso em 1º de Julho. 2009.
MATEUS, Ana. M. G. SILVA, Aparecida.
P. L. REBOLA, Célia C. C. Disponível em: http://www.educ.fc.ul.pt
Acesso em: 5 de outubro. 2009.
IFRAH, Georges. História Universal dos Algarismos: a
inteligência dos homens contada pelos números e pelo cálculo. Tomo 1. Rio
de Janeiro: Nova Fronteira, 1997.
CONWAY, Jonh H. e GUY, Richard K. - O
Livro dos Números, Col. Gradiva/Universidade de Aveiro, n.º 6, 1ª
ed., Lisboa, Gradiva, 1999.
GUELLI, Oscar. Contando a História da Matemática – A
invenção dos números. São Paulo: Ática, 2004.
IMENES, Luiz Márcio
Pereira. A numeração indo-arábica.
São Paulo: Scipione, 2002. (Coleção Vivendo a matemática).
IMENES, Luiz Márcio
Pereira. Os números na história da
civilização. São Paulo: Scipione, 1999. (Coleção Vivendo a matemática).
XIMENES, Sérgio. Minidicionário da Língua Portuguesa. Brasília: Ediouro, 2001.
Menninger, Karl. Zahlwort und Ziffer, 2ª ed. Vandenhoeck: Gottingen 1958