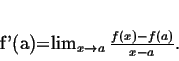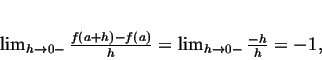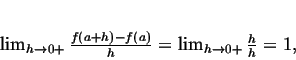CONCEITO DE LIMITES E DERIVADAS

Foi enquanto se dedicava ao estudo de algumas destas funções que Fermat deu conta das limitações do conceito clássico de reta tangente a uma curva como sendo aquela que encontrava a curva num único ponto.

Tornou-se assim importante reformular tal conceito e encontrar um processo de traçar uma tangente a um gráfico num dado ponto - esta dificuldade ficou conhecida na História da Matemática como o “Problema da Tangente”.

Estas idéias constituíram o embrião do conceito de derivada e levou Laplace a considerar Fermat “o verdadeiro inventor do Cálculo Diferencial”. Contudo, Fermat não dispunha de notação apropriada e o conceito de limite não estava ainda claramente definido.

No séc. XVII Leibniz algebriza o Cálculo Infinitesimal, introduzindo os conceitos de variável, constante e parâmetro, bem como a notação dx e dy para designar a menor possível das diferenças em x e em y. Desta notação surge o nome do ramo da Matemática conhecido hoje como “Cálculo Diferencial”.

A Teoria dos Limites, tópico introdutório é fundamental da Matemática Superior.

Portanto, o que veremos, será uma introdução à Teoria dos Limites, dando ênfase principalmente ao cálculo de limites de funções, com base nas propriedades pertinentes.

Matemático francês - Augustin Louis Cauchy – 1789/1857 foi, entre outros, um grande estudioso da Teoria dos Limites. Antes dele, Isaac Newton, inglês, 1642/1727 e Gottfried Wilhelm Leibniz, alemão, 1646/1716, já haviam desenvolvido o Cálculo Infinitesimal.

DEFINIÇÃO

Dada a função y = f(x), definida no intervalo real (a, b), dizemos que esta função f possui um limite finito L quando x tende para um valor x₀, se para cada número positivo ε , por menor que seja, existe em correspondência um número positivo δ , tal que para |x - x₀| <δ , se tenha |f(x) - L | <ε , para todo x ¹ x₀ .

Indicamos que L é o limite de uma função f( x ) quando x tende a x₀ , através da simbologia abaixo: lim f(x) = Lx® x₀

Exemplo: Prove, usando a definição de limite vista acima, que: lim (x + 5) = 8 x® 3.

Temos no caso: f(x) = x + 5 x₀ = 3L = 8.

δ = δ. Concluímos então que 8 é o limite da função para x tendendo a 3 ( x δ 3) .

O cálculo de limites pela definição, para funções mais elaboradas, é extremamente laborioso e de relativa complexidade. Assim é que, apresentaremos as propriedades básicas, sem demonstrá-las e, na seqüência, as utilizaremos para o cálculo de limites de funções. Antes, porém, valem as seguintes observações preliminares:

a) É conveniente observar que a existência do limite de uma função, quando,

x ® x₀ , não depende necessariamente que a função esteja definida no ponto x₀ , pois quando calculamos um limite, consideramos os valores da função tão próximos quanto queiramos do ponto x₀ , porém não coincidente com x₀, ou seja, consideramos os valores da função na vizinhança do ponto x₀ .Para exemplificar, consideremos o cálculo do limite da função abaixo, para x 3.

Observe que para x = 3, a função não é definida. Entretanto, lembrando que

x² - 9 = (x + 3) (x - 3), substituindo e simplificando, a função fica igual a f(x) = x + 3, cujo limite para x δ 3 é igual a 6, obtido pela substituição direta de x por 3.

b) o limite de uma função y = f(x), quando x ® x₀, pode inclusive, não existir, mesmo a função estando definida neste ponto x₀ , ou seja , existindo f(x₀).

c) ocorrerão casos nos quais a função f(x) não está definida no ponto x₀, porém existirá o limite de f(x) quando x ® x₀ .

d) nos casos em que a função f(x) estiver definida no ponto x₀ , e existir o limite da função f(x) para x ® x₀ e este limite coincidir com o valor da função no ponto x₀, diremos que a função f(x) é Contínua no ponto x₀ .

e) já vimos à definição do limite de uma função f(x) quando x tende a x₀,

ou x ® x₀ . Se x tende para x₀, para valores imediatamente inferiores a x₀, dizemos que temos um limite à esquerda da função. Se x tende para x₀, para valores imediatamente superiores a x₀, dizemos que temos um limite à direita da função.

Pode-se demonstrar que se esses limites à direita e à esquerda forem iguais, então este será o limite da função quando x ® x₀.

PROPRIEDADES OPERATÓRIAS DOS LIMITES

P1 - o limite de um soma de funções, é igual à soma dos limites de cada função.

lim ( u + v + w + ... ) = lim u + lim v + lim w + ...

P2 - o limite de um produto é igual ao produto dos limites.

lim (u . v) = lim u . lim v

P3 - o limite de um quociente de funções, é igual ao quociente dos limites.
lim (u / v) = lim u / lim v , se lim v ¹ 0.

P4 - sendo k uma constante e f uma função, lim k. f = k. lim f

Observações:

No cálculo de limites, serão consideradas as igualdades simbólicas, a seguir, envolvendo os símbolos de mais infinito ( + ¥ ) e menos infinito ( - ¥ ), que representam quantidades de módulo infinitamente grande. É conveniente salientar que, o infinitamente grande, não é um número e, sim, uma tendência de uma variável, ou seja: a variável aumenta ou diminui, sem limite.

Na realidade, os símbolos + ¥ e - ¥ , não representam números reais, não podendo ser aplicadas a eles, portanto, as técnicas usuais de cálculo algébrico.

Dado b Î R - conjunto dos números reais, teremos as seguintes igualdades simbólicas:

b + (+¥ ) = + ¥

b + ( - ¥ ) = - ¥

(+ ¥) + (+ ¥ ) = + ¥

(- ¥ ) + (- ¥ ) = - ¥

(+ ¥ ) + (- ¥ ) = nada se pode afirmar inicialmente. O símbolo ¥ - ¥ , é dito um símbolo de indeterminação.

(+ ¥ ) . (+ ¥ ) = + ¥

(+ ¥ ) . 0 = nada se pode afirmar inicialmente. É uma indeterminação.

¥ / ¥ = nada se pode afirmar inicialmente. É uma indeterminação.

No cálculo de limites de funções, é muito comum chegarmos a expressões indeterminadas, o que significa que, para encontrarmos o valor do limite, teremos que levantar a indeterminação, usando as técnicas algébricas. Os principais símbolos de indeterminação são:

¥ - ¥

¥ . 0

¥ / ¥

¥ ⁰

0 / 0

1¥

1^-¥

Cálculos de alguns limites imediatos.

a) lim (2x + 3) = 2.5 + 3 = 13

x® 5

b) lim (x² + x) = (+ ¥ )² + (+¥ ) = + ¥ + ¥ = + ¥

x® + ¥

c) lim (4 + x³) = 4 + 2³ = 4 + 8 = 12

x® 2

d) lim [(3x + 3) / (2x - 5)] = [(3.4 + 3) / (2.4 - 5)] = 5

x® 4

e) lim [(x + 3) (x - 3)] = (4 + 3) (4 -3) = 7.1 = 7

x® 4

LIMITES FUNDAMENTAIS

A técnica de cálculo de limites consiste na maioria das vezes, em conduzir a questão até que se possa aplicar os limites fundamentais, facilitando assim, as soluções procuradas. Apresentarei cinco limites fundamentais e estratégicos, para a solução de problemas.

PRIMEIRO LIMITE FUNDAMENTAL: O LIMITE TRIGONOMÊTRICO

Intuitivamente isto pode ser percebido da seguinte forma: seja x um arco em radianos, cuja medida seja próxima de zero, digamos x = 0,0001 rad. Nestas condições, o valor de senx será igual a sen 0,0001 = 0,00009999 (obtido numa calculadora científica).

Efetuando-se o quociente, vem: senx / x = 0,00009999 / 0,0001 = 0,99999 » 1. Quanto mais próximo de zero for o arco x, mais o quociente (senx) / x se aproximará da unidade, caracterizando-se aí, a noção intuitiva de limite de uma função.

Exemplo:

Uma mudança de variável, colocando 5x = u, de modo a cairmos num limite fundamental. Verifique também que ao multiplicarmos numerador e denominador da função dada por 5, a expressão não se altera. Usamos também a propriedade P4.

SEGUNDO LIMITE FUNDAMENTAL: LIMITE EXPONENCIAL

Onde e é a base do sistema de logaritmos nigerianos, cujo valor aproximado é e » 2,7182818.

Exemplo:

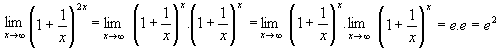
TERCEIRO LIMITE FUNDAMENTAL: CONSEQUÊNCIA DO ANTERIOR

Exemplo:

Observe o cálculo do limite abaixo:

lim (1 + x)^5/x = lim [(1 + x)^1/x]⁵ = e⁵

x® 0 ................x® 0

QUARTO LIMITE FUNDAMENTAL: OUTRO LIMITE EXPONENCIAL

Para a > 0.

QUINTO LIMITE FUNDAMENTAL

DERIVADA DE UMA FUNÇÃO Y = F(X) NUM PONTO X=X_0.

Considere a figura abaixo, que representa o gráfico de uma função y = f(x), definida num intervalo de números reais.

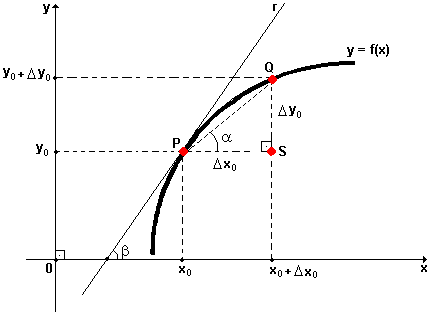
Observando a figura, podemos definir o seguinte quociente, denominado razão incremental da função:

y = f(x), quando x varia de x₀ para x₀ + D x₀ :

Define-se a derivada da função y = f(x) no ponto x = x₀, como sendo o limite da razão incremental acima, quando D x₀ tende a zero, e é representada por f ' (x₀) , ou seja:

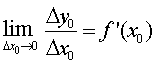
Assim, lembrando que a derivada de uma função y = f(x) pode ser indicada pelos símbolos y ‘, f ^' (x) ou dy/dx,

A seguir, uma tabela contendo as derivadas de algumas das principais funções elementares, restringindo nesta primeira abordagem, a oito funções elementares básicas, além das derivadas da soma, produto e quociente de duas funções.

FUNÇÃO	DERIVADA
y = k , k = constante	y ' = 0
y = k.x	y ' = k
y = x	y' = 1
y = xⁿ	y ' = n.x ^{n - 1}
y = a ^x , 1# a > 0	y ' = a ^x . ln a
y = e ^x	Y ' = e ^x
y = sen(x)	y ' = cos(x)
y = cos(x)	y ' = - sen(x)
y = tg(x)	y ' = sec²(x)
y = u + v	y ' = u' + v'
y = u.v	y' = u'.v + u.v'
y = u / v , v  0	y' = (u'.v - u.v') / v²

Onde u = u(x) e v = v(x) são funções deriváveis no ponto x.

Nota: a derivada de uma função y = f(x), pode ser representada também pelos símbolos: y ' ou dy/dx.

Observe que quando D x₀ ® 0 , o ponto Q no gráfico acima, tende a coincidir com o ponto P da mesma figura., definindo a reta r , que forma um ângulo b com o eixo horizontal (eixo das abscissas), e, neste caso, o ângulo SPQ = a .tende ao valor do ângulo b.

Ora, quando D x₀® 0 , já vimos que o quociente D y₀ / D x₀ representa a derivada da função y = f(x) no ponto x₀. Mas, o quociente D y₀ / D x₀ representa , como sabemos da Trigonometria, a tangente do ângulo SPQ = a , onde P é o vértice do ângulo. Quando D x₀ D 0 , o ângulo SPQ = a , tende ao ângulo b.

Assim, não é difícil concluir que a derivada da função y = f(x) no ponto x = x₀ , é igual numericamente à tangente do ângulo b . Esta conclusão será muito utilizada no futuro.

Podemos escrever então: f '(x₀) = tgb.

Conclusão importante:

A derivada de uma função y = f(x) num ponto x = x₀ coincide numericamente com o valor da tangente trigonométrica do ângulo formado pela tangente geométrica à curva representativa de y = f(x), no ponto x = x₀.

NOTA:

Uma lâmpada de um poste de iluminação pública está situada a uma altura de 6m. Se uma pessoa de 1,80m de altura, posicionada embaixo da lâmpada, caminhar afastando-se da lâmpada a uma velocidade de 5m/s, com qual velocidade se desloca à extremidade de sua sombra projetada na rua?

Considere a figura a seguir:

Supondo que a pessoa partiu do ponto O a uma velocidade de 5m/s, depois de t segundos, ela terá percorrido a distância d = 5.t e estará no ponto B.

Como a luz se propaga em linha reta, a ponta da sombra da pessoa, estará no ponto S. Seja y esta distância.

Pela semelhança dos triângulos BAS e OLS, poderão escrever:

Substituindo os valores, vem:

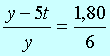
Daí, fica:

6(y – 5t) = 1,80.y

6y – 30t = 1,80y

6y – 1,80y = 30t

4,20y = 30t

y = (30/4,20)t

Portanto,

y = 7,14t

Ora, a velocidade v do ponto S será a derivada dy/dt, ou seja:

Como y = 7,14t, vem imediatamente que: .

Portanto, a velocidade do ponto extremo da sombra é igual a 7,14 m/s.

NOTA:

Um tanque tem a forma de um cilindro circular reto de raio da base r = 5m e altura

h = 10m. No tempo t = 0, o tanque começa a ser cheio com água, que entra no tanque com uma vazão de 25 m³/h. Com qual velocidade o nível da água sobe? Depois de quanto tempo o tanque estará cheio?

Considere a figura a seguir:

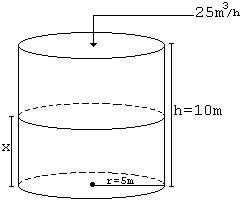
Já sabemos que o volume de um cilindro reto de raio da base R e altura h é dado pela fórmula V = p.R².h

Sendo x o nível da água no tanque, é óbvio que poderemos escrever:

V = p.5².x = 25.p.x (1)

A vazão de 25 m³/h é justamente a derivada dV/dt.

Derivando a expressão (1) em relação à x, vem imediatamente:

dV/dx = 25p

Derivando a expressão (1) em relação a t, vem:

Ora, a velocidade v com que o nível da água sobe é, exatamente dx/dt. Substituindo os valores conhecidos, vem finalmente:

25 = 25p .v, de onde tiramos v = 1/p m/h ou aproximadamente, v = 0,318 m/h. Portanto, o nível da água sobe a uma razão de 0,318 metros por hora. O tempo que levará para encher o tanque será então:

T = 10m / 0,318 m/h = 31,4h = 31h + 0,4h = 31h + 0,4. 60min

T = 31 horas e 24 minutos.

EXEMPLO:

DE COMO É USADOS LIMITE E DERIVADO NUNHAM EMPRESA FLORESTAL

A maximização do lucro (L) ocorre quando a diferença entre a receita total (RT) e os custos totais (CT) são máximos. Matematicamente, tem-se:

L = RT – CT

L = Py. Y – P_x. X

Em que P_y = preço do produto (constante); e

P_x = preço do fator (constante).

O lucro máximo é determinado no ponto em que a inclinação da função de lucro é igual a zero (primeira derivada = 0 e segunda derivada < 0).

Derivando a função de lucro em relação á do fator variável tem-se:

dL/dX = P_y. dY/dX + Y.0-P_x . dX/dX +.0

dL/dX = P_y . dY/dX - P_x

dL/dX = P_y . PFMa - P_x(6.0)

Como na equação (6.0) P_y. PFM_{a (}receita marginal) e P_x = CMa (custo marginal), tem-se:

dL/dX = RMa - CMa

Igualando a primeira derivada a zero, tem-se:

dL/dX = RMa– CMa = (6.1)

A equação (6.1) pode ser escrita da seguinte forma:

RMa = CMa = 0 ou

RMa = CMa ou (6.3)

VPFMa = P_x(6.4)

Em que VPFMa = valor do produto físico marginal.

Admitindo-se que a segunda derivada da função de lucro seja menor que zero, as equações (6.3) e (6.4) determinam que o lucro será máximo quando o retorno obtido ao produzir uma unidade a mais do produto for igual ao custo para produzir essa unidade a mais.

O quadro abaixo ilustra a maximização de lucro da empresa florestal onde o custo marginal do fator, ou preço do fator (P_x1), é igual a US$ 2,00 e o preço do produto (P_y) igual a US$ 2,00.

X₁	Y	PFMe	PFMa	CMa(P_x1)	VPFMa	CT	RT	Lucro
1	1	1,0	1	2	2	2	2	0
2	3	1,5	2	2	4	4	6	2
3	6	2,0	3	2	6	6	12	6
4	10	2,5	4	2	8	8	20	12
5	15	3,0	5	2	10	10	30	20
6	19	3,2	4	2	8	12	38	26
7	22	3,1	3	2	6	14	44	30
8	24	3,0	2	2	4	16	48	32
9	25	2,8	1	2	2	18	50	32 *
10	25	2,5	0	2	0	20	50	30

*Ponto em que o lucro é máximo

DEFINIÇÃO DE DERIVADA E REGRA DE DERIVAÇÃO

Tomemos os coeficientes angulares, m (x) = (f (x) – f (a))/(x – a), também chamados declividades, das retas secantes a G (f) por (x, f (x)) e (a, f (a)). Se a reta limite de nossas considerações preliminares existir e não for vertical, significa que os coeficientes angulares m (x) tendem a um valor fixo, m (a), que é o coeficiente angular da reta tangente e que chamaremos derivada de f em a. Na definição precisa, a seguir, o ponto a é ponto de:

$A\subset\mathbb R$

e também ponto de acumulação de A.

Isto é, lembrando que A denota o conjunto dos pontos de acumulação de A, impomos.

$a\in A\bigcap A'$

Definição 3.1.1

Consideremos uma função $a\in A\bigcap A'$ e $f:A\to \mathbb R$ A função f é derivável em a, se existir o limite

$\begin{displaymath} f'(a)=\lim_{x\to a} \frac{f(x)-f(a)}{x-a}. \end{displaymath}$

(3.2)

Neste caso, o valor f' (a) é chamado derivada de f em a.

Há várias notações para a derivada. Sendo y = f (x), as seguintes são algumas das mais comuns:

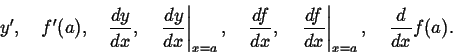
$\begin{displaymath}y',\quad f'(a),\quad \frac{dy}{dx},\quad \left.\frac{dy}{dx}... ...\left.\frac{df}{dx}\right\vert _{x=a},\quad \frac{d}{dx}f(a). \end{displaymath}$

O termo diferenciável é sinônimo de derivável e também será usado de agora em diante com a mesma liberdade com que passaremos de uma para qualquer outra das notações acima.

A notação dy/dx é devida a Leibnitz. No seu tempo a formalização do conceito de limite não havia sido atingida e o uso dessa notação pode ser explicado da seguinte forma:

O acréscimo da variável x

$\Delta x=x-a$

Produz um acréscimo da variável y,

$\Delta y=y-b:=f(a+\Delta x)-f(a)$ .

A idéia é que, ao se tornarem infinitamente pequenos esses acréscimos passavam a ser denotados por dx e dy, respectivamente, e operavam-se com eles formalmente como com dois números quaisquer.

A razão $x\in A$

Transformava-se em dy/dx e este símbolo não representava um nem outro, como acontece hoje, mas o quociente entre dy e dx. A despeito desses argumentos não ter uma clara fundamentação lógica, devem ser julgados no contexto de sua época.

A notação de Leibnitz permanece e notará que ela é útil sendo, em muitas circunstâncias, a mais sugestiva.

A notação f' (x) é atribuída a Lagrange. É a notação mais conveniente quando f é diferenciável em um conjunto A e se considera a função derivada em A. Isto é, a função f' que associa a cada

$x\in A$

a derivada f'(x) de f no ponto x. Quando a variável independente representa o tempo e é indicada por t, também se usa para a derivada de y = f (t) a notação

$\dot y$ , atribuída a Newton.

Após as considerações feitas até aqui é natural colocar:

Definição 3.1.2

Sendo y = f (x) derivável em a, a reta tangente ao gráfico, G (f), em (a, b), b = f (a), é a reta dada por:

y - b = f (a)(x - a).

Se a equação horária de um movimento retilíneo é x = s (t), onde s é uma função diferenciável da variável tempo t, a velocidade v(t₀) num instante t₀ é a derivada de s em t₀, isto é, v (t₀): = s (t₀).

Exemplo 3.1.1

(1) Se, $f(x)=k \ (constante)$ então f (x) = 0. De fato, neste caso, o limite (1.1) fica

$\begin{displaymath}\lim_{x\to a}\frac{k-k}{x-a}=0 \end{displaymath}$

em qualquer ponto a.

(2) Se f (x) = x², então f' (a) = 2a. De fato,

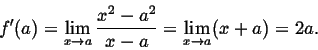
$\begin{displaymath}f'(a)=\lim_{x\to a}\frac{x^2-a{}^2}{x-a} = \lim_{x\to a}(x+a)= 2a. \end{displaymath}$

(3) A reta tangente à parábola y = x², no ponto (2,4) é:

y – 4 = 4(x – 2).

(3.3)

De fato, a derivada de x² no ponto x = 2 é igual a 4. Usando agora o fato de que a equação da reta de coeficiente angular m, passando pelo ponto (a,b), é dada por y – b = m (x-a)

Chega-se à equação (3.3).

(4) Generalizando o item (2), tem-se:

$\begin{displaymath}(x^n)' = n x^{n-1} , \quad n=1,2, \ldots. \end{displaymath}$

Antes de provarmos esse fato, convém observar que, se f é uma função diferenciável em um ponto a, na definição de derivada, o limite (1.1) pode ser escrito na forma:

$\begin{displaymath}f'(a)= \lim_{h\to0}\frac{f(a+h)-f(a)}h, \end{displaymath}$

O que será feito com muita freqüência daqui a diante.

Retomando o nosso exemplo, aplicando o desenvolvimento do binômio obtemos:

$\begin{displaymath}\begin{split} (x^n)' &=\lim_{h\to 0}\frac{(x+h)^n - x^n} h \... ...n-2} h + \ldots + h^{n-1} ] \\ &= n x^{n-1}. \end{split} \end{displaymath}$

Para n = 1, temos um caso particular importante dessa fórmula:

(x) = 1,

Isto é, a derivada da função identidade é 1. A fórmula neste caso faz sentido apenas para:

$x\ne0$

uma vez que a expressão 0⁰ não é definida. Entretanto, pode verificar diretamente, a partir da definição de derivada, que (x) = 1, inclusive no ponto x = 0.

(5) $\text{\rm sen}'x = \cos x$ . De fato, usando o Primeiro Limite Fundamental para justificar a penúltima e a última linha da seguinte cadeia de igualdades, tem:

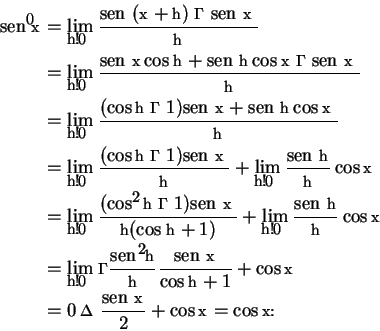
$\begin{displaymath}\begin{split} \text{\rm sen}'x &= \lim_{h\to0} \frac{\text{... ...cdot\frac{\text{\rm sen}\ x}2 + \cos x = \cos x. \end{split} \end{displaymath}$

(6)

$\cos'x= -\text{\rm sen}\ x$ Deve-se encarregar da demonstração desse fato.

Definição 3.1.3

Se a função:

$f:A\to \mathbb R$ e derivável em cada ponto de um conjunto

$B\subset A$

diz-se que f é derivável (ou diferenciável) em B. Se tivermos A = B, diremos simplesmente que f é derivável.

Assim, as funções:

$\text{sen}$ , $\cos$ e y = xⁿ, $n\in{\mathbb N}$

são exemplos de funções diferenciáveis. A seguinte proposição e os próximos dois exemplos ajudam a entender como deve ser uma função não diferenciável.

Proposição 3.1.1

Se uma função f é derivável em um ponto a, então f é contínua em a.

Prova.

Note que f é contínua em a se, e somente se,

$\begin{displaymath}\lim_{h\to0}\left[f(a+h)-f(a)\right]=0.\end{displaymath}$

Este, de fato, é o caso quando f é diferenciável em a, pois:

$\begin{displaymath}\lim_{h\to0}\left[f(a+h)-f(a)\right] = \lim_{h\to0}\frac{f(a+h)-f(a)}hh = f'(a)\cdot0 = 0. \end{displaymath}$

Como estou interessado em entender como é uma função não diferenciável num ponto, posso reformular a Proposição 3.1.1 dizendo que toda função descontínua num ponto a é não diferenciável em a.

A pergunta agora é: vale a recíproca da Proposição 3.1.1? Ou seja, será que toda função contínua em a é diferenciável nesse ponto?

A resposta é negativa (como era de se esperar, pois em caso afirmativo, os conceitos de diferenciabilidade e continuidade seriam equivalentes e poderíamos ficar com apenas um deles). Os exemplos seguintes mostram funções contínuas e não diferenciáveis em um ponto.

As funções diferenciavam formam, portanto, uma classe mais seleta, ser diferenciável é ser contínua e mais alguma coisa.

Exemplo 3.1.2

A função f (x) = |x| é contínua, mas não diferenciável, no ponto a = 0. De fato, neste caso, o limite (3.2) em a = 0, calculado à esquerda e à direita, assume valores distintos:

$\begin{displaymath} \lim_{h\to0-}\frac{f(a+h)-f(a)}h = \lim_{h\to0-}\frac{-h}h=-1, \end{displaymath}$	(3.4)
$\begin{displaymath} \lim_{h\to0+}\frac{f(a+h)-f(a)}h = \lim_{h\to0+}\frac hh=1, \end{displaymath}$	(3.5)

logo, não existe f' (0).

As expressões (3.4) e (3.5) são chamadas, respectivamente, derivada à esquerda e derivada à direita de f em 0. São denotadas por f (0 -) e f' (0 +). Considerando limites laterais em (3.2) e lembrando as propriedades desses limites temos: Seja a um ponto do domínio de uma função f e também ponto de acumulação lateral desse domínio, deixando-o à esquerda e à direita. f é diferenciável em a se, e somente se, suas derivadas laterais existem e coincidem.

Neste caso, f' (a) = f (a-) = f (a +).

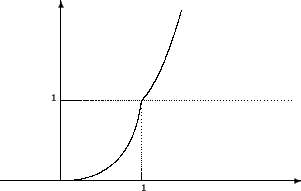
Exemplo 3.1.3. A função:

$f(x)=\min\{x^2,x^4\}$ é contínua, mas não diferenciável, nos pontos $a=\pm1$

Deixamos ao leitor, como exercício, a verificação da continuidade de f. A não diferenciabilidade em a=1 é conseqüência da propriedade que enunciamos acima a respeito das derivadas laterais. De fato, como x⁴< x², para – 1 < x < 1, e x²< x⁴, para x > 1, usando o mesmo raciocínio do Exemplo 3.1.2, obtemos:

$f' ( 1- ) = 4 \neq 2 = f' ( 1+ )$ .

O dispondo de mais de um recurso para verificar a não diferenciabilidade em a = - 1, inclusive o de explorar o fato de ser f uma função par. Por isso deixamos essa tarefa a seu encargo como exercício.

$\min\{x^2,x^4\}$

$\includegraphics{figdois3.eps}$

O gráfico acima representa a função do Exemplo 3.1.3. Observando essa figura, bem como o gráfico de f (x) = |x|, e refletindo um pouco sobre uma possível recíproca da Proposição 3.1.1, o concluiremos que ela é inviável. Além das descontinuidades, os pontos onde o gráfico apresenta uma quina, “uma situação de não concordância”, são pontos onde não existe reta tangente ao gráfico, embora tenhamos continuidade da função nesses pontos.

Numa linguagem intuitiva, estas são situações típicas de não diferenciabilidade, enquanto que, grosso modo, o gráfico de uma função diferenciável tem um aspecto suave, não anguloso, como o gráfico de f (x) = x³ ou das funções $\text{sen}\ x$ ou $\cos x$ , por exemplo.