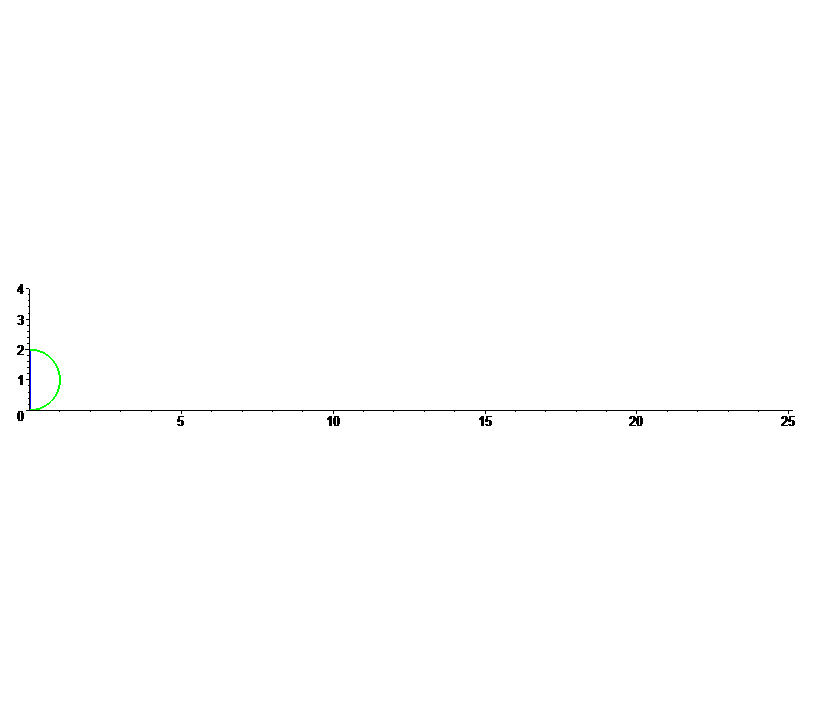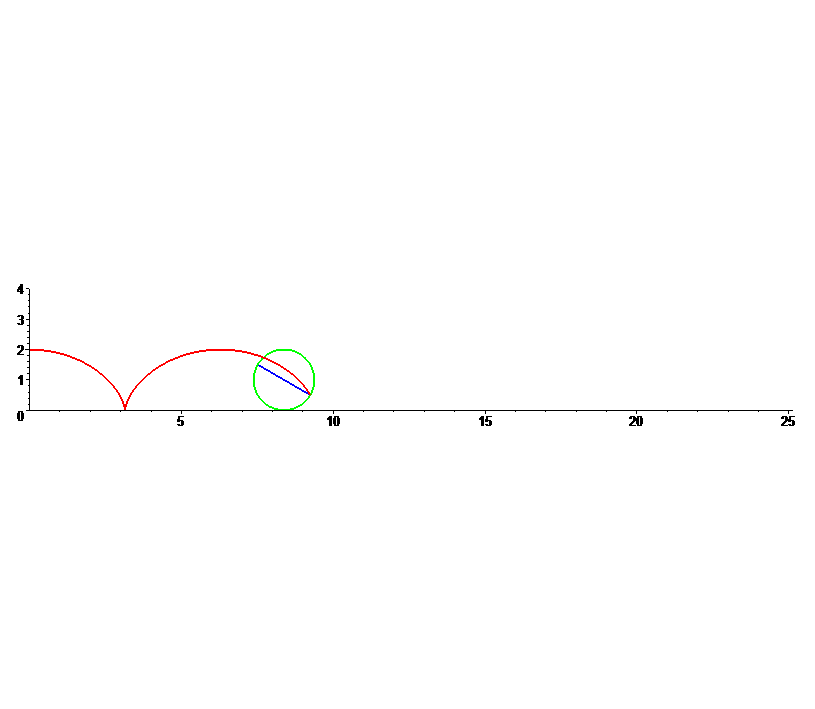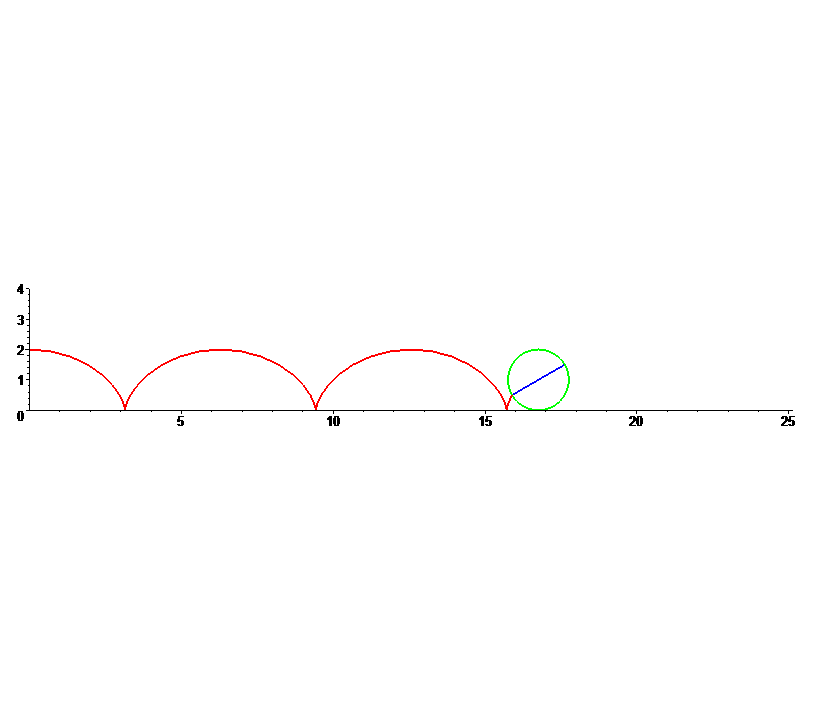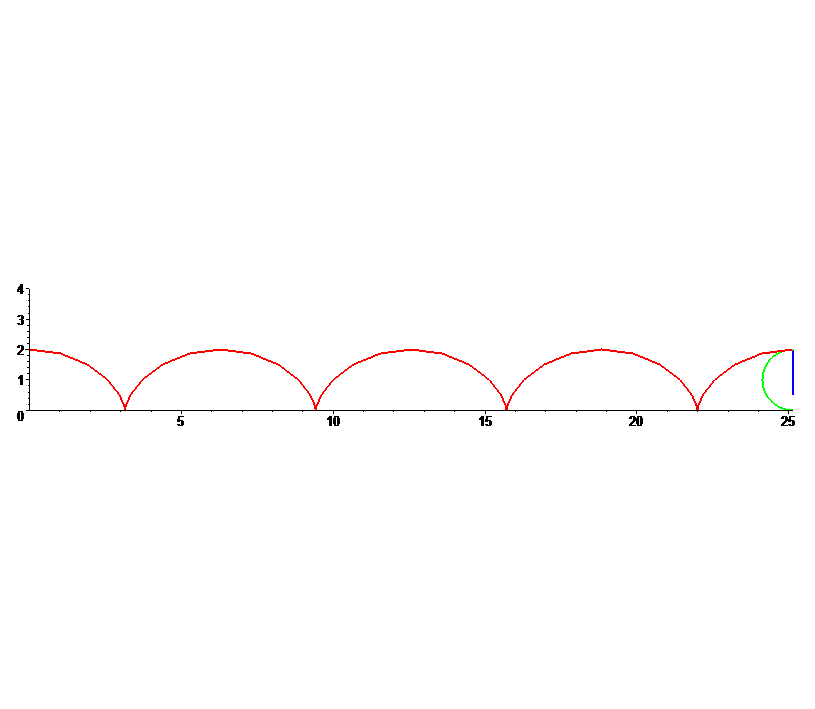
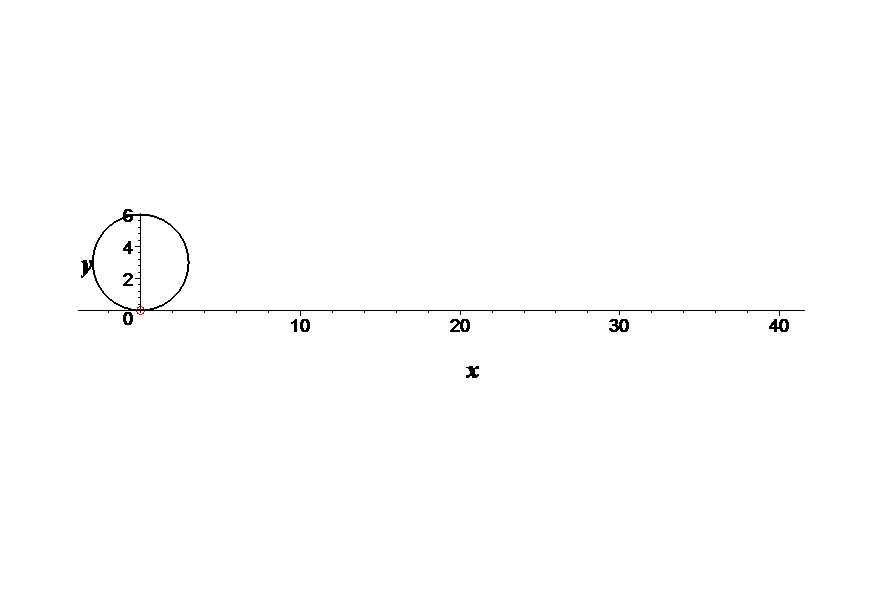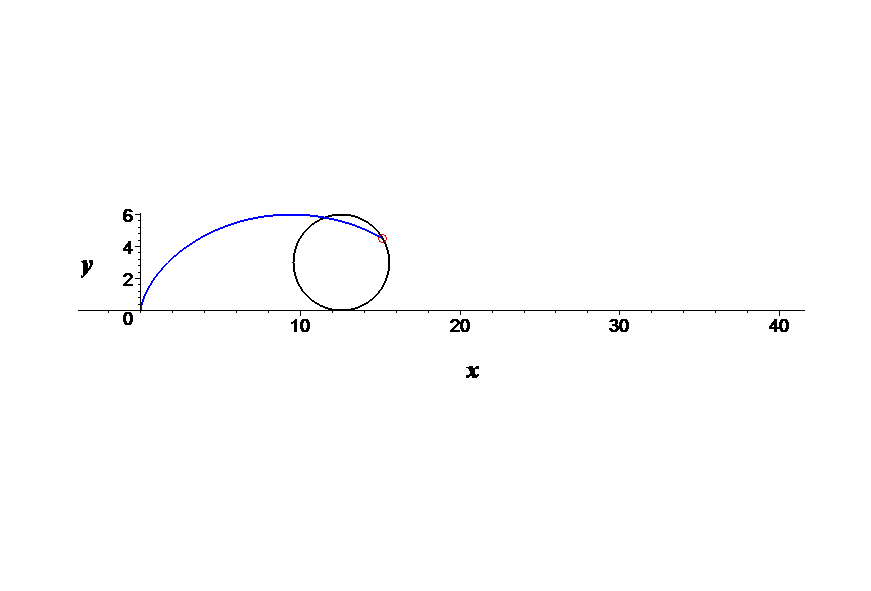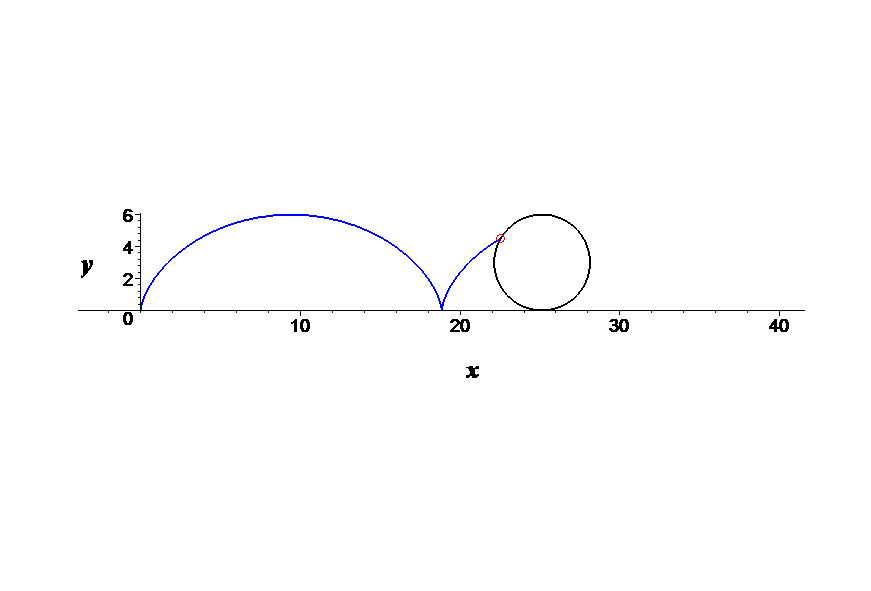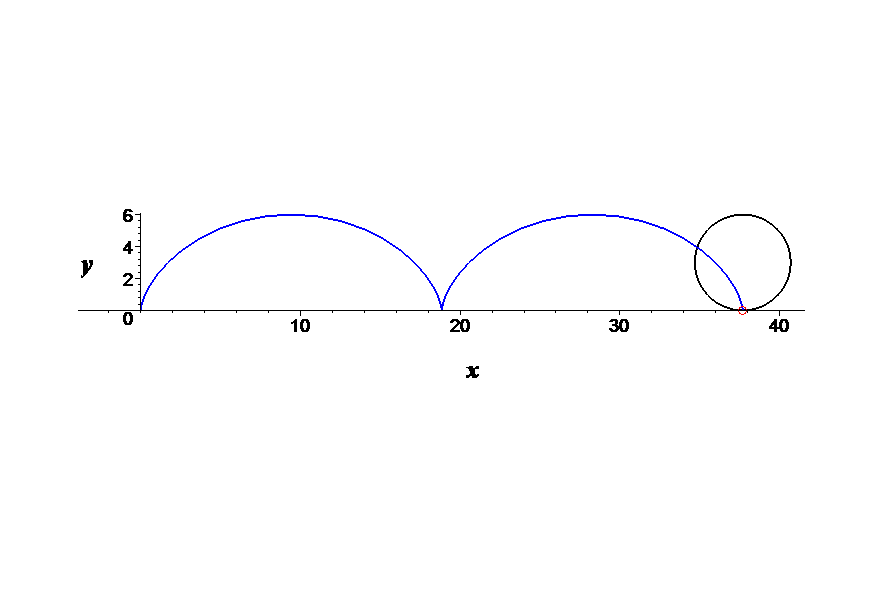

Suponhamos que o disco rola ao longo do eixo OX, da esquerda para a direita, começando na origem.
Consideremos o ponto P no topo do disco na sua posição inicial. O objectivo é encontrar a fórmula paramétrica
para a trajectória de P quando o disco rola, em função do raio
r do disco e da velocidade angular w (em radianos por segundo).
O movimento do ponto P pode ser decomposto numa translação e numa rotação. A translação de P é igual à translação do centro do disco. Para deduzirmos esta, notemos que o número de revoluções como função do tempo t é igual a
w t
revoluções = ------
2 Pi
Então a translação horizontal do centro no instante t é o número de revoluções vezes o perímetro do disco, 2 Pi r, e a translação vertical é 0:
translação = [2 Pi r revoluções, 0] = [r w t, 0]
Deduzamos agora o movimento de P devido à rotação. Porque o disco rola para a direita, e o ponto de partida é o topo do disco, medimos o ângulo de rotação w t relativamente ao eixo OY. Então a rotação é dada por
rotação:= [r sin(w t), r cos(w t)]
O movimento ciclóide de P é a soma vectorial da sua translação e da sua rotação, ajustado verticalmente pelo raio r, pois o disco rola em cima do eixo OX.
cicloide = translação + rotação + [0, r] = [r sin(w t) + r w t, r + r cos(w t)]