ILOG CPLEX provides a facility for entering a problem in a natural, algebraic LP formulation from the keyboard. The problem can be modified and saved from within ILOG CPLEX. This procedure is one way to create a file in a format that ILOG CPLEX can read. An alternative technique is to create a similar file using a standard text editor and to read it into ILOG CPLEX.
The ILOG CPLEX LP format is provided as an input alternative to the MPS file format. An LP format file may be easier to generate than an MPS file if your problem already exists in an algebraic format or if you have an application which generates the problem file more readily in algebraic format (such as a C application). Working with LP Files explains the implications of using LP format rather than MPS format.
ILOG CPLEX accepts any problem saved in an ASCII file provided that it adheres to the following syntax rules.
-
Anything that follows a backslash (\) is a comment and is ignored until a return is encountered. Blank lines are also ignored. Blank lines and comment lines may be placed anywhere and as frequently as you want in the file.
-
In general, white space between characters is irrelevant as it is skipped when a file is read. However, white space is not allowed in the keywords used to introduce a new section, such as
MAX, MIN, ST, or BOUNDS. Also the keywords must be separated by white space from the rest of the file and must be at the beginning of a line. The maximum length for any name is 255. The maximum length of any line of input is 510.
Skipping spaces may cause ILOG CPLEX to misinterpret (and accept) an invalid entry, such as the following:
If the user intended to enter that example as a nonlinear constraint—not valid in LP format—ILOG CPLEX would instead interpret it as a constraint specifying that one variable named
x1x2 must be equal to zero.
To indicate a quadratic constraint in this section, use explicit notation for multiplication and exponeniation (not space).
-
The problem statement must begin with the word
MINIMIZE or MAXIMIZE, MINIMUM or MAXIMUM, or the abbreviations MIN or MAX, in any combination of upper- and lower-case characters. The word introduces the objective function section.
-
Variables can be named anything provided that the name does not exceed 255 characters, all of which must be alphanumeric (a-z, A-Z, 0-9) or one of these symbols: ! " # $ % & ( ) , . ; ? @ _ ` ' { } ~. Longer names are truncated to 255 characters. A variable name can not begin with a number or a period.
The letter
E or
e, alone or followed by other valid symbols, or followed by another
E or
e, should be avoided as this notation is reserved for exponential entries. Thus, variables can not be named
e9,
E-24,
E8cats, or other names that could be interpreted as an exponent. Even variable names such as
eels or
example can cause a read error, depending on their placement in an input line.
-
The objective function definition must follow
minimize or maximize. It may be entered on multiple lines as long as no variable, constant, or sense indicator is split by a return. For example, this objective function 1x1 + 2x2 +3x3 can be entered like this:
but not like this:
1x1 + 2x
2 + 3x3 \ a bad idea
|
because the second style splits the variable name
x2 with a return.
-
The objective function may be named by typing a name and a colon before the objective function. The objective function name and the colon must appear on the same line. Objective function names must conform to the same guidelines as variable names (Rule 4). If no objective function name is specified, ILOG CPLEX assigns the name
obj.
-
The constraints section is introduced by the keyword
subject to. This expression can also appear as such that, st, S.T., or ST. in any mix of upper- and lower-case characters. One of these expressions must precede the first constraint and be separated from it by at least one space.
-
Each constraint definition must begin on a new line. A constraint may be named by typing a name and a colon before the constraint. The constraint name and the colon must appear on the same line. Constraint names must adhere to the same guidelines as variable names (Rule 4). If no constraint names are specified, ILOG CPLEX assigns the names
c1, c2, c3, etc.
-
The constraints are entered in the same way as the objective function; however, a constraint must be followed by an indication of its sense and a right-hand side coefficient. The right-hand side coefficient must be typed on the same line as the sense indicator. Acceptable sense indicators are <, <=, =<, >, >=, =>, and =. These are interpreted as
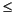 ,
, 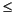 ,
, 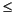 ,
, 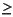 ,
, 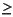 ,
, 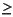 , and =, respectively.
, and =, respectively.
For example, here is a named constraint:
Quadratic constraints are allowed in this section. They are specified inside square brackets
[]. All quadratic coefficients must appear inside square brackets. Multiple square bracket sections may be specified. Inside of the square brackets, two variables are multiplied by an asterisk (
*).
-
The optional
bounds section follows the mandatory constraint section. It is preceded by the word bounds or bound in any mix of lower- and upper-case characters.
-
Each bound definition must begin on a new line. The format for a bound is ln
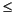 xn
xn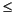 un except in the following cases:
un except in the following cases:
Upper and lower bounds may also be entered separately as
ln
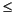
xn
xn
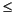
un
with the default lower bound of 0 (zero) and the default upper bound of +
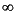
remaining in effect until the bound is explicitly changed.
Bounds that fix a variable can be entered as simple equalities. For example,
x5 = 5.6 is equivalent to
5.6 <= x5 <= 5.6.
The bounds +
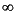
(positive infinity) and -
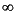
(negative infinity) must be entered as words:
+infinity,
-infinity,
+inf,
-inf.
A variable with a negative infinity lower bound and positive infinity upper bound may be entered as
free, in any mix of upper- and lower-case characters, with a space separating the variable name and the word
free. For example,
x7 free is equivalent to
- infinity <= x7 <= + infinity.
-
The file must end with the word
end in any combination of upper- and lower-case characters, alone on a line, when it is created with the enter command. This word is not required for files that are read in to ILOG CPLEX, but it is strongly recommended. Files that have been corrupted can frequently be detected by a missing last line.
-
This rule applies to the ILOG CPLEX MIP optimizer. To specify any of the variables as general integer variables, add a
GENERAL section; to specify any of the variables as binary integer variables, add a BINARY section. The GENERAL and BINARY sections follow the BOUNDS section, if one is present; otherwise, they follow the constraints section. Either of the GENERAL or BINARY sections can precede the other. The GENERAL section is preceded by the word GENERAL, GENERALS, or GEN in any mix of upper- and lower-case characters which must appear alone on a line. The following line or lines should list the names of all variables which are to be restricted to general integer values, separated by at least one space. The BINARY section is preceded by the word BINARY, BINARIES, or BIN in any mix of upper- and lower-case characters which must appear alone on a line. The following line or lines should list the names of all variables which are to be restricted to binary integer values, separated by at least one space. Binary variables are automatically given bounds of 0 (zero) and 1 (one), unless alternative bounds are specified in the BOUNDS section, in which case a warning message is issued.
Here is an example of a problem formulation in LP format where
x4 is a general integer:
Maximize
obj: x1 + 2 x2 + 3 x3 + x4
Subject To
c1: - x1 + x2 + x3 + 10 x4 <= 20
c2: x1 - 3 x2 + x3 <= 30
c3: x2 - 3.5 x4 = 0
Bounds
0 <= x1 <= 40
2 <= x4 <= 3
General
x4
End
|
If branching priorities, branching directions, or special ordered sets exist, enter this information through ORD and SOS files, as documented in
ORD File Format and
SOS File Format.
-
This rule applies to the ILOG CPLEX MIP optimizer. To specify any of the variables as semi-continuous variables, that is as variables that may take the value
0 or values between the specified lower and upper bounds, use a SEMI-CONTINUOUS section. This section must follow the BOUNDS, GENERALS and BINARIES sections. The SEMI-CONTINUOUS section is preceded by the keyword SEMI-CONTINUOUS, SEMI, or SEMIS. The following line or lines should list the names of all the variables which are to be declared semi-continuous, separated by at least one space.
-
This rule applies to the ILOG CPLEX MIP optimizer. To specify special ordered sets, use an SOS section, which is preceded by the SOS keyword. The SOS section should follow the Bounds, General, Binaries and Semi-Continuous sections. Special ordered sets of type 1 require that, of the variables in the set, one at most may be non-zero. Special ordered sets of type 2 require that at most two variables in the set may be non-zero, and if there are two non-zeros, they must be adjacent. Adjacency is defined by the weights, which must be unique within a set given to the variables. The sorted weights define the order of the special ordered set. For MIP branch and cut, the order is used to determine how the variables are branched upon. See the CPLEX User's Manual for more information. The type of set is specified by either of the S1 or S2 keywords followed by a double colon. The set member names are listed on this line or lines, with their weights. Variable names and weights are separated by a colon, for example:
-
This rule applies to the ILOG CPLEX barrier optimizer for quadratic programming problems (QPs). Quadratic coefficients may appear in the objective function. (If there are quadratically constrained variables in the problem, see rule 4, rule 9, and Solving Problems with Quadratic Constraints (QCP) in the CPLEX User's Manual)
The algebraic coefficients of the function x'Qx are specified inside square brackets
[]. The square brackets must be followed by a divide sign followed by the number 2. This convention denotes that all coefficients inside the square brackets will be divided by 2 in evaluating the quadratic terms of the objective function. All quadratic coefficients must appear inside square brackets. Multiple square bracket sections may be specified.
Inside of the square brackets, two variables are multiplied by an asterisk (
*). For example,
[4x*y] indicates that the coefficients of both of the off-diagonal terms of Q, corresponding to the variables
x and
y in the model are 2, since
4x*y equals
2x*y + 2x*y. Each pair of off-diagonal terms of Q is specified only once. ILOG CPLEX automatically creates both off-diagonal entries of Q. Diagonal terms in Q (that is, terms with an exponent of 2) are indicated by the carat (
^) followed by 2. For example,
4x^2 indicates that the coefficient of the diagonal term of Q corresponding to the variable
x in the model is 4.
For example, this problem
Minimize |
|
|
|
|
|
|
|
|
|
|
|
a |
+ |
b |
+ |
1/2 |
(a2 |
+ |
4ab |
+ |
7b2) |
subject to |
|
|
|
|
|
|
|
|
|
|
|
a |
+ |
b | |
10 |
|
|
|
|
|
|
a, |
b | |
0 |
|
|
|
|
|
|
in LP format looks like this:
Minimize
obj: a + b + [ a^2 + 4 a * b + 7 b^2 ]/2
Subject To
c1: a + b >= 10
End
|
 PREVIOUS
NEXT
PREVIOUS
NEXT
 PREVIOUS
NEXT
PREVIOUS
NEXT
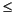 ,
, 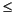 ,
, 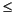 ,
, 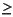 ,
, 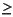 ,
, 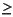 , and =, respectively.
, and =, respectively.
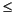 xn
xn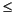 un except in the following cases:
un except in the following cases:
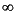 remaining in effect until the bound is explicitly changed.
remaining in effect until the bound is explicitly changed.
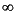 (positive infinity) and -
(positive infinity) and -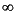 (negative infinity) must be entered as words:
(negative infinity) must be entered as words: